近年来,伴随着越来越多的轨道交通线路建成并投入使用,线网规模逐步扩大,运营管理模式也向着网络化运营方向发展,现有的分线运营模式已无法满足运营管理的需求。因此,为了提高城市轨道交通网络化运营的效率,提升客运服务水平,十分有必要从网络化运营的角度出发,以换乘节点作为着力点,基于换乘衔接对列车运行计划进行协调优化。本文在分析网络运行计划协调的特征与方法、换乘时间组成与影响因素的基础上,以平峰期乘客平均换乘等待时间最小为目标,建立基于换乘衔接的列车运行计划协调模型,并利用粒子群算法对模型进行求解,使各线路列车运行计划在换乘节点良好衔接,实现城市轨道交通平峰时段的网络运行计划协调优化。
1 换乘时间分析
在采用“一票换乘”的轨道交通系统中,乘客购票进站后,搭乘列车到达换乘站下车后,可直接通过通道、站台等换乘到目标站台搭乘接续列车,到达目的地并刷卡出站。因此,乘客换乘时间包括走行时间、等待时间。走行时间主要受走行速度、距离、换乘便利性等影响,取决于乘客的个体属性(如年龄、身体状况等)、站台空间分布和换乘方式;等待时间主要受所乘线路列车在换乘站的衔接状态影响,衔接状态良好,乘客到达目标站台即可搭乘列车,无需等待,而衔接状态不佳,乘客到达站台时列车恰好离开,则需等待下一趟列车。因此,在协调过程中,应合理安排列车在换乘站的衔接状态,尽可能避免出现乘客恰好错过列车的情况,减少乘客的换乘等待时间,进而提高网络化运营的效率,提升服务水平。
2 基于网络协调的平峰期列车换乘衔接模型
2.1 基本假设
本文以平峰时段的列车运行计划协调优化作为研究目标,在建立优化模型前,做出如下假设:在协调时段内,线网中列车运行参数(如区间运行时间、行车间隔等)已知,且不随时间变化;换乘需求较为稳定且分布均匀,各换乘关系的客流量及平均换乘走行时间已知,且基本稳定;模型不考虑同一线路上下行方向之间的换乘;假定换乘乘客均搭乘第一趟目标列车离站。
2.2 模型建立

2.3 模型求解
本文建立的基于换乘衔接的列车运行计划协调模型,可利用粒子群算法进行求解。模型的决策变量为全线网中各线路各方向一趟列车在某换乘站的发车时刻,设线网中有n条线路,则决策变量有2n个,通过初始化随机生成决策变量,选取目标函数作为适应度评价函数,代入计算全网平均换乘等待时间,根据全局最优结果和个体最优结果对随机决策变量进行更新,不断进行迭代计算,求得使全网平均换乘等待时间最小的最优解。
3 算例

3.2 求解结果与分析
本文基于MATLAB平台建立模型并求解计算。粒子群算法的相关参数设置情况如表2所示。在协调的过程中,取各站换乘走行时间为3.5min,换乘缓冲时间为1min,迭代300次后,求解得到协调结果如表3所示,平均换乘等待时间随迭代次数增加的变化曲线如图2所示,协调结果与实际情况的对比如表4所示。

表3 协调前后各线进入协调时段首列车在各换乘站的发车时刻
| 换乘站 | 线路方向 | 协调前 | 协调后 |
| A | 11 | 10:01:30 | 10:04:00 |
| A | 12 | 10:03:00 | 10:00:00 |
| A | 21 | 10:04:00 | 10:04:00 |
| A | 22 | 10:00:30 | 10:04:00 |
| B | 11 | 10:00:30 | 10:03:00 |
| B | 12 | 10:04:00 | 10:01:00 |
| B | 31 | 10:01:00 | 10:00:00 |
| B | 32 | 10:02:48 | 10:04:00 |
| C | 21 | 10:00:00 | 10:00:00 |
| C | 22 | 10:04:30 | 10:00:00 |
| C | 31 | 10:05:00 | 10:04:00 |
| C | 32 | 10:04:48 | 10:00:00 |
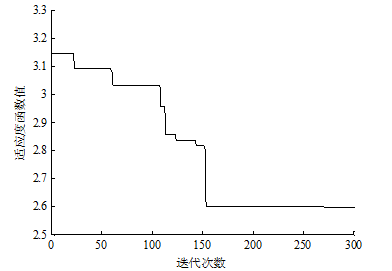
图2 平均换乘等待时间随迭代次数增加的变化曲线
表4 协调前后乘客换乘等待时间对比
|
| 换乘客流量(人) | 总换乘等待时间(min) | 平均换乘等待时间(min) |
| 协调前 | 8520 | 26673 | 3.131 |
| 协调后 | 8520 | 22125 | 2.597 |
| 优化量 |
| 4548 | 0.534 |
由图2可知,通过300次迭代后,目标函数收敛于2.597。通过表4对比分析可知,对于该协调时段,换乘客流总量为8520人,协调前全网平均换乘等待时间为3.131分钟,总换乘等待时间为26673分钟,协调后全网平均换乘等待时间为2.597分钟,全网的总换乘等待时间为22125分钟。与协调前相比,协调结果使全网总换乘等待时间减少了4548分钟,平均换乘等待时间减少了0.534分钟。由于该算例中的线网规模和换乘客流量较小,故对于平均换乘等待时间协调优化幅度较小,当优化线网规模较大时,相应的换乘客流量也会增大,优化效果会更显著。
4 结论
本文从网络协调的角度出发,以全网平均换乘等待时间最小化为目标,构建了基于换乘衔接的列车运行计划协调模型,并利用粒子群算法求解。同时,以深圳地铁实际运营为背景,通过算例验证了模型与算法的有效性,通过协调减少全网平均换乘等待时间,提升换乘效率与服务水平。本文对列车运行计划协调问题进行了初步的探讨,后续研究可考虑乘客个体属性、列车运行延误等随机因素的影响,进行深入研究与改进,进一步提高协调的效果,提升换乘效率。
参考文献
[1]Wu J,Liu M,Sun H,et al.Equity-based timetable synchronization optimization in urban subway network[J].Transportation Research Part C Emerging Technologies,2014,(15).
[2]马超云.城市轨道交通换乘站列车时刻表的协调和优化[D].北京:北京交通大学,2010.
[3]Wong,Rachel C.W.,Yuen,Tony W.Y.,Fung,Kwok Wah.Optimal Timetable Synchronization for Rail Mass Transit [J].Transportation Science,2008,42(1).
[4]张铭,杜世敏.基于递阶偏好的轨道交通网络化运营换乘协调优化[J].铁道学报,2009,31(6).
[5]白广争,郭进,石红国,等.基于离站时刻协调的地铁换乘站列车衔接优化研究[J].交通运输系统工程与信息,2013,13(5).
[6]刘建华.粒子群算法的基本理论及其改进研究[D].长沙:中南大学,2009.
基金项目:教育部人文社科基金项目(15YJCZH108);广东省自然科学基金项目(2015A0303103)。
收稿日期:2017-10-16
作者简介:邝永松(1975-),男,广东广州人,深圳地铁运营总部路网指挥中心运营协调部副经理,工程师、研究方向:轨道交通运营组织管理。








