太阳能光伏系统是通过太阳能组件将太阳能转化成电能的一种新型能源系统。利用光伏技术可实现太阳能发电,具有环保、节能、美观、安全、经济等优点。为了保证光照,光伏组件一般安装在建筑屋顶。由于屋顶长期处在阳光直射、雨水、高空大风等恶劣的环境中,如果支撑框架不牢固,组件很有可能会被大风刮落,影响行人安全,因此对光伏组件支撑框架的牢固性要求比较高。采用有限元模型对光伏一体化屋面的光伏组件和支撑框架之间的关系进行分析是非常有必要的。
1 有限元模型介绍
有限元计算模型时将求解区域看作有多个互连单位组成的整体单元,利用该模型可将基本方程分片(子域)近似解计算出来,考虑到单元(子域)可被划分成各种大小和形状不一的尺寸,因此可用来对一些外形结构比较复杂的材料进行计算。有限元分析法主要是采用变分原理和加权余量法来进行计算,利用有限元分析方法可将整个计算单元划分成多个小单元,然后从各个小单元中选出相应的节点来对函数插值点来进行求解。有限元分析法作为一种现代化结构分析算法,当前常用的算法主要有CAWS法、WAWA法、小波法、逆傅里叶法、线形回归滤波器法等。在采用有限元分析模型进行分析时,WAWA算法和CAWS算法需要的计算量比较大,在进行计算时没有对时间和风速之间的关联性进行考虑。而选用线性回归法进行分析则更为合理,采用线性回归过滤器模拟技术可结合风向脉动风情况将各个脉动风节点的等效惯性计算出来,并利用ANSYS软件计算出随机振动,从而将光伏组件和支撑框架之间的关系建设出来。
2 计算方法
在分析一体化屋面光伏组件和支撑框架之间的关系时,使用随机模拟时程分析法对时域进行分析。具体的分析步骤如下:(1)结合风荷载统计特点,人工生成了具有空间相关性和特定频谱密度风速时程,然后转化成风压作用到支撑框架结构上;(2)时域的运动方式可采用Newmari逐步积分法来进行计算求解,将不同时间节点的反应情况计算出来;(3)多获得的样本进行统计分析,进而计算出均值。
3 采用ANSYS算法进行分析
采用ANSYS算法编制出来的模拟程序可计算出具体的风速时程数据,并利用Fortran程序将风速转化成各个连接节点,并根据计算后得到的结果使用ANSYS实施计算。
3.1 计算假设
(1)在进行计算时,无需对风力作用和支撑结构的耦合影响进行分析;(2)只分析光伏组件顺风方向上的振动情况;(3)在进行计算时,无需分析屋面结构产生振动后对组件和框架的之间的影响进行分析;(4)需利用三维模型分析光伏组件和支撑框架之间的空间行和相关性进行分析。
3.2 模型以及参数
在进行计算时,光伏组件的方钢设计尺寸为45mm×45mm×5mm,方钢主要用作立柱。横梁选用2L25mm×3mm角钢构成导T型截面钢,屋面端部位置横梁选用变长相等的角钢,角钢的尺寸为L25mm×3mm,设计单块光伏组件尺寸为1.58m×0.807m。在光伏组件中,按照《剥离幕墙工程技术规范》(JGJ102-2003)中的要求选择建筑玻璃幕墙的相关参数。
在进行计算时,梁单元和柱子单元使用beam4单元,光伏组件中玻璃幕墙选用shell63单元,详细分析了上述两种模型:(1)详细分析和计算了幕墙玻璃的位移和应力,详细分析计算了单块光伏模型组件,将组件模型划分成100个板单元;(2)对框架柱、框架梁的位移和应力进行计算,然后使用整体框架模型,将组件按照2m×2m划分成4个单元,分别将各柱和各梁划分成2个梁单元。设计的基本模型参数如表1所示。
表1 基本模型参数
| L/m | 1.580 | B/m | 0.808 |
| 体型系数(按荷载规范) | 1.3 | 风向角/(°) | 0 |
| 屋面高度H/m | 20 | 坡度i/(°) | 30 |
| M/kg.m-2 | 15 | 立柱高h/mm | 250 |
| 风速谱函数 | Davenport谱 | 地貌类别 | B类 |
3.3 光伏组件和支撑框架瞬态分析
在对光伏组件和支撑框架进行瞬态分析时,分别对30m/s、25m/s、20m/s这3种工况风速的瞬态位移进行模拟分析,每次分析间隔0.02s,模拟的时间为60s,设计回归阶次为4次,按照规范要求设计风载体型系数为1.3,顺风向使用dav-enport谱。按照风速的不同,采用大挠度理论开展非线性分析,并对风力影响下光伏组件的振动情况进行分析,然后将节点上的气从属面积和风压相乘后得出结构等效惯性力。
以30m/s风速情况下光伏组件节点位移时程曲线为例开展分析,光伏组件中幕墙玻璃会在和板的方向保持垂直的方向上出现振动。平均风速为30m/s、25m/s、20m/s时的具体计算结果见表2。
表2 光伏组件产生的位移情况和应力情况
| 平均风速/kg.m-1 | 位移方差值/mm | 位移值/mm | 瞬时时间/s | 最大位移值/mm | Mises应力/MPa |
| 20 | 1.21 | 2.43 | 4.20 | 7.07 | 18.5 |
| 25 | 1.83 | 3.81 | 0.12 | 10.26 | 28.7 |
| 30 | 2.31 | 5.0 | 18.24 | 12.13 | 34.7 |
经过分析发现,在脉动风作用下光伏组件的均值、位移方差和应力相应都会随着风速的增加而增加。在进行计算时,详细分析了施工过程中钢化玻璃几何非线性,并得到了光伏组件和风速之间的关系,通过分析发现,两者未出现二次抛物线的关系。而且在风速不断增大的情况下,位移会逐步趋于缓和。
从表3可以看出,在其他参数保持一致时,随着风速的不断增大,整体支撑框架柱子、梁受脉动风的影响位移值和应力值都会随之增加,而且在组件周围的应力值会达到最大值,并集中出现在跨中位置,对支撑框架产生了影响。所以,在施工时,要合理地选择梁柱截面,尤其是要注意边柱、端柱、边梁等位置。
表3 支撑框架梁位移和应力
| 脉动风平均风速/kg.m-1 | 位移方差/mm | 位移均值/mm | 最大位移/mm | 出现时间/s | 梁Mises应力/MPa | 柱Mises应力/MPa |
| 20 | 1.00 | 1,99 | 5.48 | 4.20 | 133.8 | 27.3 |
| 25 | 1.48 | 3.08 | 0.12 | 8.30 | 215.1 | 60.6 |
| 30 | 1.89 | 4.33 | 9.92 | 18.24 | 286.3 | 65.1 |
3.4 分析光伏组件和支撑框架之间的风振系数
在进行计算时,常用的风振系数主要包括位移风振系数和内力风振系数。本文在进行研究时,重点对位移风振系数进行分析和研究。在实际分析时,将位移

3.4.1 单个光伏组件模型峰值系数分析
采用式(1)将平均风速为30m/s的单板块各节点沿边长的均值、方差和风振系数如图1所示,板的挠度情况和位移方差值挠度情况比较相似,单块屋面板在峰值因子为3.0时节点位移风振系数变化比较均匀,取值的变化范围处于2.4~2.6。
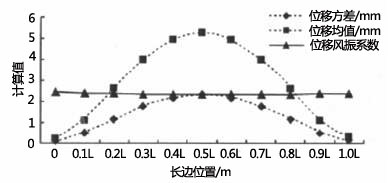
图1 单块板各个节点位移方差、均值和风振系数曲线
3.4.2 整体框架模型风振系数
采用式(1)对平均风速为30m/s时的光伏组件和支撑框架的有限元模型进行了分析,得到沿长边榀中间榀每一跨位移风振系数曲线如图2所示。
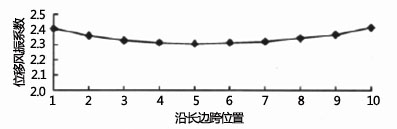
图2 整体模型位移风振系数曲线
从图2可以看出,中间榀位移风振系数<整个模型边榀框架产生的风振系数,模型整体位移风振系数变化值非常小。一般来说,边跨位移风振系数为2.41,中间跨位移系数为2.32。根据分析结果,为了方便工程施工过程中进行使用,可将支撑框架结构和光伏组件结构的风振系数保持在2.3~2.6。
4 结语
综上所述,采用有限元计算模型分析光伏一体化屋面光伏组件和支撑框架之间的关系后发现,在不同风荷载的影响下,光伏组件中的内力均保持在支撑框架允许的最大值内,在平均风速为30m/s时光伏组件产生的位移最大值为12.13mm,位移量远远<规范要求的支撑框架最短变长1/60的刚度要求。由于支撑框架梁截面相对来说较小,平均风速为30m/s时,梁端位置的最大瞬时应力值>289MPa,需重点考虑,尤其是要考虑梁端节点位置连接处。在实际施工时,为了方便施工,设计将支撑框架结构和光伏组件的风振系数值取为2.3~2.6。
参考文献
[1]杨赛亮.光伏一体化屋面支撑框架与屋面结构层连接的有限元分析[D].杭州:浙江工业大学,2013.
[2]杨小攀.工业厂房光伏屋面一体化设计及结构抗震性能研究[D].绵阳:西南科技大学,2016.
(作者李新转供职于海南英利新能源有限公司)








