近年来,随着天然气的普及,未来供气格局将发生变化,管道气将成为人们生活中的主要气源。尽管如此,在短期内瓶装液化气仍将继续发挥燃气供给的重要作用,因此液化气供应站仍将承担着瓶装液化气的主要供给责任。为了节省成本,提高配送效率,供应站的数量及位置尤为重要。为解决这些问题,文章提出一种利用大数据技术的液化气供应站的优化选址算法,对供应站的地域覆盖程度、最短路径进行量化计算,并预测出最佳供应站数量。在实际运用中,可结合主观经验和本文提出的优化选址算法,为液化气增减供应站提供精准决策支持。
1 供应站优化选址模型研究
液化气供应站选址的主要考虑因素为地域覆盖度、布设区域的用户购买量、交通便利程度、安全性、运营成本等。本文提出的优化选址方法,是利用液化气的现有数据,对布设液化气供应站的考虑因素进行量化分析,分别建立地域覆盖度模型、最短路径模型及非线性支持向量机预测模型,进而建立基于大数据的液化气供应站优化选址模型。
1.1 地域覆盖度模型
首先,需要考虑每个站点与其他相邻站点间的空间距离。一般而言,每个供应站应尽量覆盖多的用户。如果相邻供应站距离太近,就会产生覆盖地域重合,所以应将各个供应站尽量分散,以确保利用有限数量的供应站尽可能覆盖更多的区域。本文提出了一个地域覆盖度模型,利用供应站空间布局特点,量化一个供应站对应的地域覆盖程度。
现有的每一个供应站都有一个实际的物理地址。应利用地址解析算法将地址信息转换成经纬度信息。选取某一参考点作为坐标原点,进一步将经纬度信息转换成空间位坐标置,并以此计算空间距离。

1.2 最短路径模型
由于成本、道路交通、地理环境等原因,供应站不可能随意进行布设,因此交通便利性也是布设供应站的一个重要因素。在交通便利的区域设置供应站,能够为液化气的配送提供便利,提高配送效率。
距离矩阵逐次求解,n为网络节点数,x先为网络权矩阵,然后组成迭代矩阵,算法如下:
function d=fld(n,x)
for r=1:n
for i=1:n
for j=1:n
p(j)=x(i,j)+x(j,r)
end
d(r,i)=min(p)
end
end

2 供应站优化选址模型的实证分析
本文以我国S市为例,采用上述方法及步骤对液化气供应站优化选址模型进行实证分析。实验验证数据采用液化气集团的数据,为实际的布设及数量增减提供直观的数据支持。
图1为S市的某地区的供应站图。根据数据统计,该区域内液化气供应站数量为12个,标为站点A,B,C,…,L。

图1 S市某地区供应站分布图
利用公式计算该地区内的12个供应站地域覆盖度,并计算相应的供应站到街道的距离。
创建12×12矩阵,并任一元素赋初值为inf(无穷大);d=ones(12);d=inf×d;逐点填写分段权,输入网络权矩阵。
d=Columns1through11(2220,2620,2620,1420,1420,1820,1400,1480,1640,1640,1420)
然后考虑订单量、用户数的变化趋势,运用非线性支持向量机预测模型,预测出在该地区最佳的供应站数量为2个。
再根据之前计算出的最短路径,最终选定为S、H两个站点,其余的A、F、G、J合并至B供应站,C、E、D、I、K、L合并至H供应站。合并之后的站点将扩大业务量,如图2所示。

图2 减少后的供应站分布图
S市原有供应站约124个,根据现有的历史数据,运用相应模型预测出未来几年的供应站数量趋势图,如图3所示。
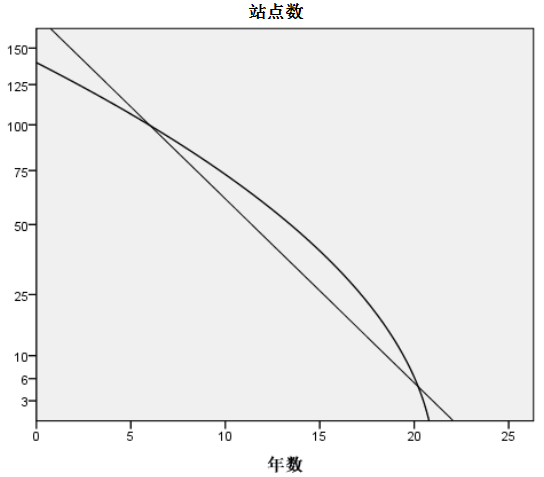
图3 供应站数量趋势变化图
从图3曲线可以看出,液化气供应站的数量逐年递减,目前日常订单量稳定的供应站站点约为10个,预计未来10年随着天然气的普及,液化气供应站的数量仍将进一步减少。
3 结语
本文提出一种大数据下的液化气供应站选址方法,对供应站的数量位置考虑了地域覆盖度、交通便利度及最短距离、订单量、用户数等因素,并进行量化建模,预测出最佳位置以及供应站数量。在减少大量人工调研成本的同时,为液化气供应站的布设提供数据化的决策支持。
参考文献
[1]孙亚夫,陈文斌.基于分词的地址匹配技术[C].中国地理信息系统协会年会,2007.
[2]孙志超.瓶装燃气供应站规划的新思考——以深圳市为例[C].中国城市规划年会,2012.
[3]王铁宁,裴帅,陈春良.基于二元语义群决策的油料供应站选址方法[J].装甲兵工程学院学报,2009,23(5).
[4]罗雪晖,李霞,张基宏.支持向量机及其应用研究[J].深圳大学学报,2003,20(3).
[5]呼文亮,王惠文.基于贝叶斯准则的支持向量机预测模型[J].北京航空航天大学学报,2010,36(4).
(作者姚晓鹏供职于上海申腾信息技术有限公司)








