铁磁颗粒增强橡胶复合材料的力学性能探究

0　引言

进入21世纪以来，世界面临着资源进一步枯竭的严峻现状，材料的运用被大大限制。复合材料的出现，让材料科学焕发出新生命。铁磁颗粒增强橡胶复合材料由此氤氲而生，被广泛应用于航空航天、汽车、电子电气、建筑、健身器材等领域。

铁磁颗粒增强橡胶的复合材料是一种由磁性颗粒和非磁性基体弹性材料组成的新型复合材料，具有可控的剪切特性、阻尼特性等，并可以在外场激励下产生大应变、复杂变形、迅速响应等诸多优点，在减振降噪、智能材料与智能驱动等领域具有广泛的应用前景，是一类新兴的磁性智能复合软材料。

在工程应用中，绝大多数天然橡胶和合成橡胶都需要填充一定的炭黑、铁颗粒等各种填料，以此改善强度、硬度、加工性能等特性。通常来说，颗粒增强复合材料随着增强颗粒尺寸改变，体积占比的大小以及颗粒材料的不同都会对复合材料的一系列宏观和微观性能产生显著的影响和改变，如能够改变材料密度、弹性模量、剪切模量、外观、应变灵敏性、屈服强度、绝热性等。

中国科技大学龚兴龙研究小组对铁磁颗粒增强橡胶复合材料的制备工艺、微观机理、性能分析及应用等方面进行了研究，建立了磁流变弹性体力学性能测量系统；周刚毅、冯青、王凯强等利用有限元软件对铁磁颗粒增强橡胶复合材料在多物理场条件下的拉伸、剪切性能做了初步分析。虽然铁磁颗粒增强橡胶复合材料已经在多个领域得到了较好的应用，但我国对铁磁颗粒增强橡胶复合材料的研究相对起步较晚，尚未形成系统的研究理论。

1　力学特性探究

1.1　研究内容

本文研究铁磁颗粒增强橡胶力学性能在不同颗粒半径、不同颗粒体积分数以及颗粒不同排列方式等情况下的影响，得到的结果将作关于理论值与实验值、各向同性和各向异性、不同颗粒半径影响等的对比。体积分数以每3%为一个单位，从0～30%变化的各向同性分布的力学性能并进行相关数据的比较。

1.2　基本假设

在铁磁颗粒增强橡胶复合材料中，铁磁颗粒在基体中是呈链状或柱状结构排列，而且材料的应力分布受到颗粒体积分数的显著影响。利用COMSOL有限元分析软件建立在稳态情况下的单元体模型，研究颗粒在不同体积分数、不同粒径大小和排列方式上对铁磁颗粒增强橡胶复合材料的力学特性的影响。基于以下假设建立颗粒增强橡胶复合材料的细观力学模型：

（1）基体和颗粒材料是均匀的、连续的。

（2）颗粒和基体不因泊松比不同而引起横向变形，忽略泊松效应。

（3）颗粒、基体和复合材料的应力应变都满足线弹性条件，即服从虎克定律。

（4）颗粒和基体紧密接触，内部结构受力时不产生相对滑动，满足变形一致条件。

（5）由于研究的是颗粒分布方式不同对基体弹性模量以及剪切模量的影响，所以需要考虑到各向同性以及各向异性的问题。

（6）铁磁颗粒单链完整，链中颗粒间距相等。

（7）各链无限长，链间平行排列，在纵向均匀分布。

1.3　材料参数

材料参数见表１。

表1　材料参数

	杨氏模量E/Pa	泊松比	密度/（kg/m3）
铁磁颗粒	2e11	0.291	7860
橡胶基体	2.14e6	0.48	1000

1.4　理论值

Mori-Tanaka模型相当于能量法里面解决夹杂平均应变的，表现物理含义的方法，其更好地考虑了夹杂物与基体之间的相互作用。通过Mori-Tanaka方法可计算各向同性相关的剪切模量及体积模量，公式为：

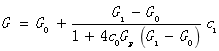
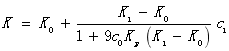
其中：

        

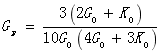
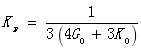
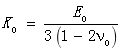
而拉应力和应变可以通过竖向拉伸指定位移或加载一定的力来计算得到，剪切应力与应变由切向指定位移加载一定力来计算得到。

1.6　模型与边界条件

1.6.1　模型建立

在COMSOL软件中建立模型通过改变颗粒间距来控制铁磁颗粒的体积分数，铁磁颗粒的半径为3μm和8μm，对于各向异性，给定橡胶基体是长度和宽度均为20μm的长方体。

基于前文假设，本文建立单元模型如下：颗粒组成的单链沿纵向排列，从单链中取出仅含有一个铁磁颗粒成为要研究的单元体，如图1所示。

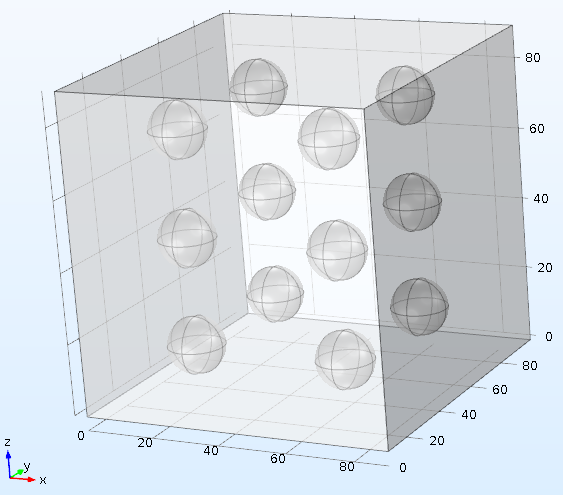
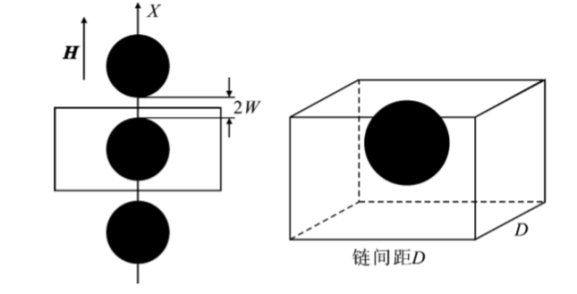
图1　单元模型

假设单元体的长度、宽度为D，高度H=2W+2R，其中R为颗粒的半径，2W为上下相邻的两颗粒之间的间距。因此，材料的颗粒体积分数之间的关系式为：

 

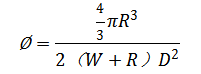
若D=2（W+R），单元体为正方体，即为各向同性的单元体。

1.6.2　边界条件设置

为了求得弹性模量E，将单元体置于三维直角坐标系中，定义单元体的边界条件如下：单元体在XOZ平面与其平行的对面、YOZ平面与其平行的对表面所对应的四个面均设置为周期性边界条件。单元体顶面设置大小为2μm的纵向位移，将底面XOY平面固定。为避免有限元分析出现不收敛的情况，还需在底面再加一个边的固定约束。

同理，为了计算剪切模量，定义单元体的边界条件如下：单元体在XOZ平面与其平行的对面、YOZ平面与其平行的对表面所对应的4个面均设置为周期性边界条件。只需要将单元体顶面边界设置改为大小为2μm的切向位移，并将底面XOY平面固定，以搓动位移产生剪切效应，得到相关数值。

1.7　有限元结果分析

1.7.1　各向同性有限元数据结果

建立铁磁颗粒半径为3μm和8μm，体积分数从0～30%的不同的立方单元体模型，在COMSOL稳态力学研究模块中添加上述边界条件后进行计算，获得模型整体相关的力学性能运算结果，在派生值中获取每个体积分数下对应的应力及应变数值，进而计算得出对应情况的弹性模量E和剪切模量G。图2展示两种体积分数在有限元计算中的应力状态。

 

 

3%体积分数拉伸应力分布

 

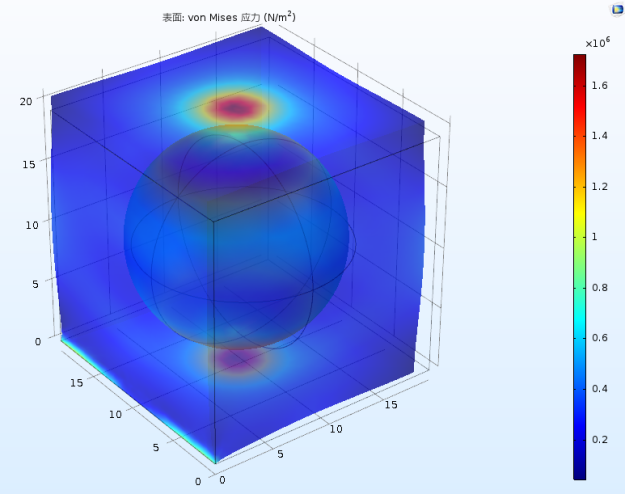
30%体积分数拉伸应力分布

图2　两种体积分数的应力图

通过派生值获取其应力、应变，并计算得到两种不同颗粒半径在不同体积分数下的结果如图3、图4。

 

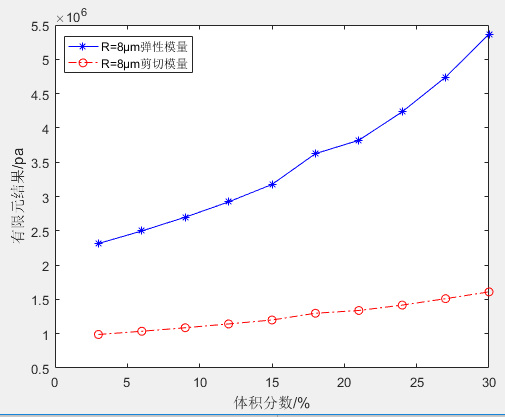
图3　R=8μm弹性模量和剪切模量

 

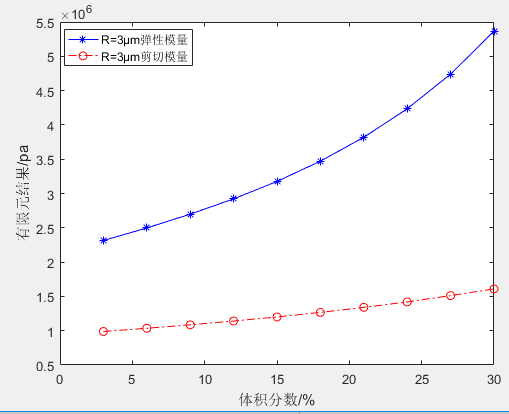
图4　R=3μm弹性模量和剪切模量

1.7.2　各向异性有限元数据结果

 

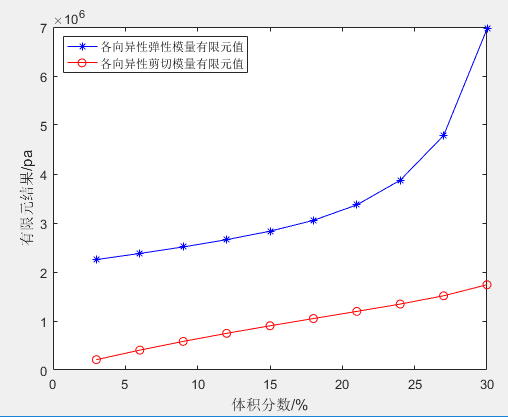
图5　R=8μm各向异性弹性模量、剪切模量

 

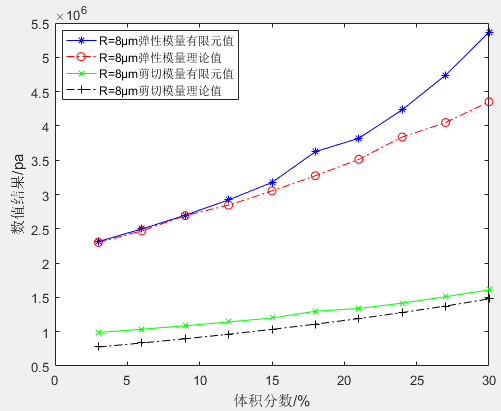
图6　R=8μm弹性模量、剪切模量对比

1.7.3　各向同性理论值与有限元结果对比

在MATLAB中进行数值模拟后，将各向同性分布的有限元结果和M-T方法计算出的理论值进行对比，可以更直观地看出有限元值与理论值的区别。弹性模量在低体积分数时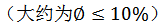，理论值与实验值相差很小，当体积分数增大后，实验值与理论值的差距逐渐增大；对剪切模量而言，有限元值通常比理论值大一些，但是其随体积分数变化的趋势是一致的，如图6所示。

1.7.4　各向同性不同粒径对比

通过弹性模量和剪切模量数值拟合图形可以很直观地看出虽然颗粒半径不同，但是所体现的力学性能是几乎一致的。因此，可以认为颗粒半径不影响该复合材料的力学性能，只由体积分数来改变性能。两种粒径结果对比如图7所示。

 

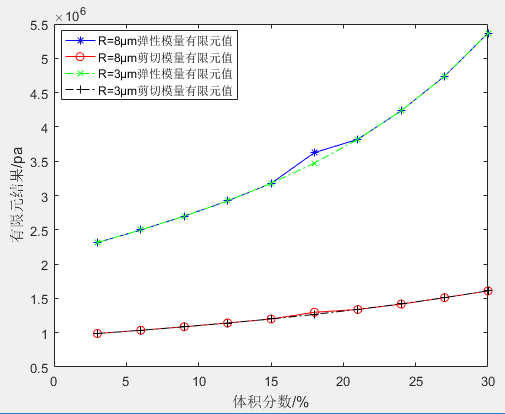
图7　不同尺寸的实验结果对比

1.7.5　各向异性与各向同性对比

本节将各向同性和各向异性的材料性能作了对比，对于弹性模量，可以看出当体积分数较大时，各向异性材料特性随体积分数的增大其变化趋势将更大，当体积分数较小时，两种材料的特性变化趋势接近。对于剪切模量，各向异性材料在低体积分数时，其值很小，但随着体积分数增大，其数值增大趋势较快；各向同性材料低体积分数时剪切模量稍大，但随着体积分数增加，变化要缓慢一些。

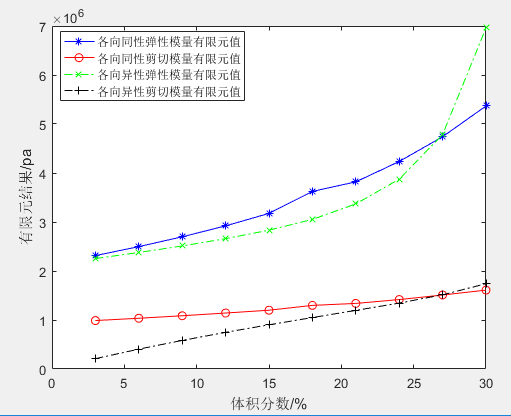
图8　各向同性和各向异性实验结果对比