1 概述
齿轮传动作为机械传动中应用最广泛的一种传动方式，目前广泛应用于航天、航空和航海等诸多机械领域，其性能对整个传动系统的可靠性具有重要影响。同时，齿轮啮合可靠性与相关人员的安全息息相关，故对齿轮啮合接触应力进行较为合理的分析研究，进而指导各部件的设计研发，具有重要意义。
国内外许多专家和学者已对直齿圆柱齿轮啮合过程中的接触应力进行了大量的研究，但大多基于确定性分析方法，即忽略了相关变量的不确定性对接触应力的影响，其研究结果不具有普遍性，不能很好地指导齿轮部件的设计和研发。因此，为了更客观准确地描述齿轮啮合过程中接触应力的分布，提高齿轮传动的可靠性能，应考虑齿轮啮合接触应力相关影响因素的随机性，这就要求将齿轮啮合接触应力的确定性分析转变为可靠性分析。
概率分析方法在许多领域已有广泛应用，但目前还没有应用于啮合齿轮接触应力的可靠性分析。对啮合齿轮接触应力进行概率分析，不但可以根据随机变量的分布特征得到啮合齿轮接触应力的概率分布特性，而且可以根据啮合齿轮接触应力的概率分布特征确定随机变量的变化情况，有利于啮合齿轮的设计优化，也有助于改善齿轮传动系统的可靠性能。本文在有限元分析的基础上，应用蒙特卡罗方法（Monte Carlo Method，MCM）和响应面方法（Response Surface Method，RSM）相结合的混合响应面方法，考虑直齿圆柱齿轮啮合阶段的非线性时域内随机变量对接触应力的影响，对直齿圆柱齿轮接触应力进行非线性可靠性灵敏度分析。
2 混合响应面法
3 直齿圆柱齿轮非线性分析
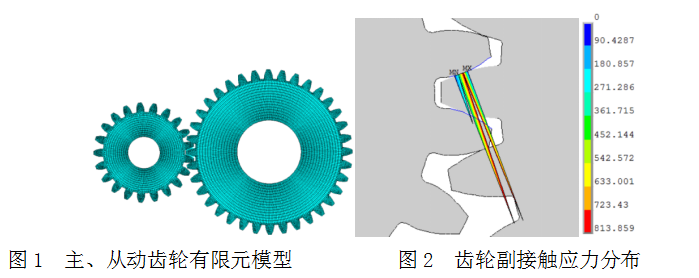
选取某航空发动机减速器直齿圆柱拟合齿轮，根据分析问题的需要，对主、从动齿轮模型进行适当简化。为了提高计算效率，用面模型代替体模型反映两个轮齿啮合过程中接触应力的分布，利用ANSYS软件建立有限元模型，如图1所示。选取面单元PLANE182对啮合齿轮模型划分网格，共生成13407个节点和11344个单元。
选取主、从动齿轮的一对轮齿啮合过程中从开始啮合到完成啮合这一时域[0，1]（秒）作为分析范围，这一时域内轮齿之间的啮合过程可以视为非线性问题处理。选取20CrMnTi渗碳钢为主、从动齿轮的材料，其屈服强度为850MPa（GB/T3077-1988），齿轮尺寸参数和材料属性详见表1，对这一问题进行有限元分析，通过在两个齿轮副之间插入一个接触对实现两个轮齿之间的动态接触，得到主、从动齿轮啮合时的接触应力云图，如图2所示，两个齿轮副啮合过程中，最大接触应力为813.859MPa。
4 直齿圆柱齿轮接触分析可靠性灵敏度分析
4.1 可靠性灵敏度数学模型
4.2 可靠性分析
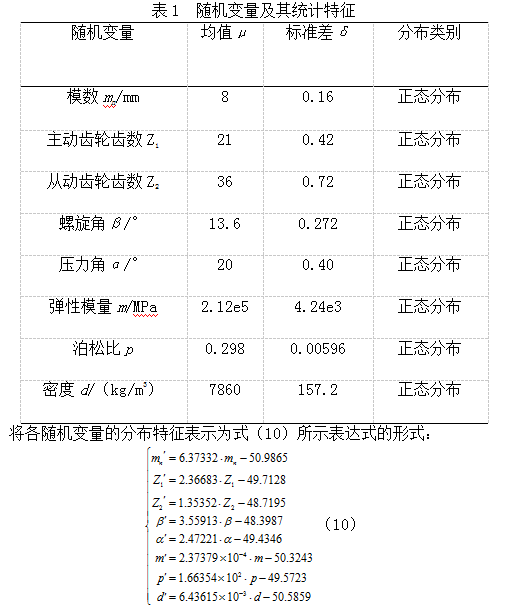
对主、从动齿轮非线性分析的基础上，对齿轮副啮合过程中的接触应力进行概率分析。综合考虑影响接触应力分布的关键因素，将齿轮关键尺寸参数（模数、齿数、螺旋角、压力角）和材料属性（弹性模量、泊松比、密度）设为随机变量且相互独立，其统计特征见表1：
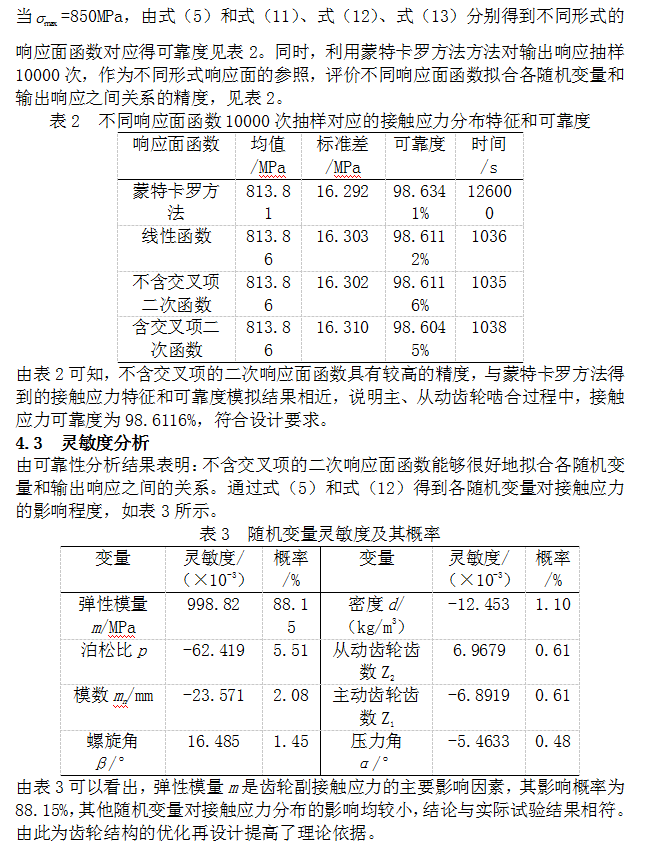
采用蒙特卡罗方法和拉丁超立方体抽样方法对各随机变量进行抽样，得到80组随机变量和输出响应样本点。利用这些样本点拟合响应面函数，为了进一步研究响应面函数形式（线性函数、不含交叉项二次函数、含交叉项二次函数）对输出响应分布特征的影响，拟合线性响应面函数、不含交叉项响应面函数、含交叉项响应面函数，分别如
式（11）、式（12）和式（13）：
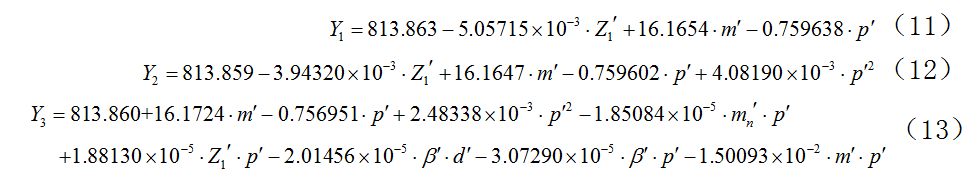
运用响应面函数对啮合齿轮做进一步仿真，得到10000次模拟输出样本。由式（11）、式（12）和式（13）响应面函数得到对应的输出样本历史和输出响应概率分布，分别如图3、图4和图5所示：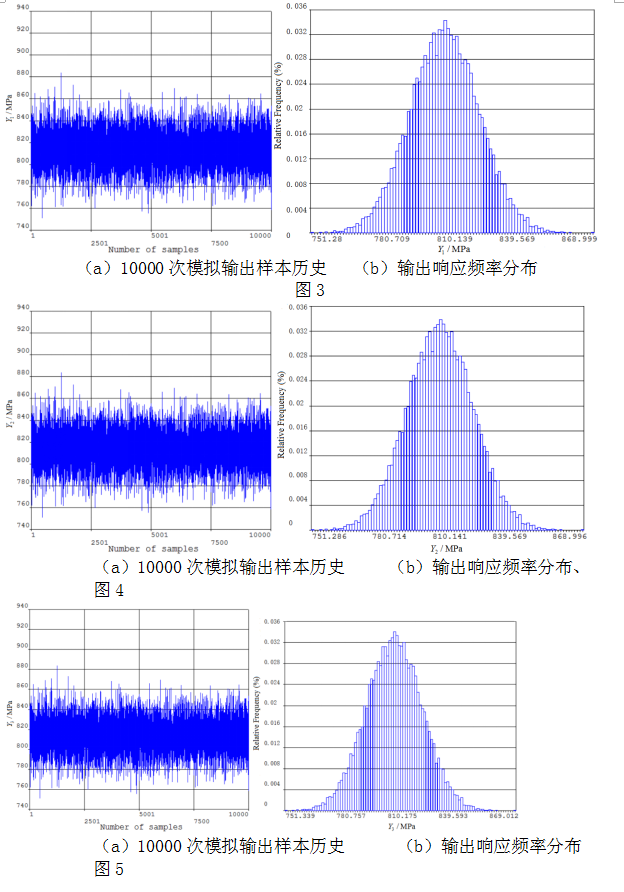
5 结语
（1）通过对直齿圆柱齿轮副啮合过程中的非线性接触应力的分析，初步研究了接触应力的分布特征，选取最大接触应力为输出响应对齿轮副接触应力进行了概率分析。
（2）通过对齿轮副接触应力概率和随机变量灵敏度的分析，可知：对于最大极限应力
=850MPa，安全概率为98.6116%，基本符合设计要求。同时，得出了接触应力分布的主要影响因素，为齿轮结构的优化在设计提供了理论依据。
（3）通过不同形式响应面函数与蒙特卡罗方法对比，评估了蒙特卡罗方法和不含交叉项二次函数结合的混合响应面法的精度和效率，阐述了混合响应面方法的有效性，为复杂结构输出响应非线性概率分析提供有效方法。
参考文献
[1]尉晓霞，任家骏，林卫虹，等．直齿圆柱齿轮三维接触应力边界元分析[J]．太原理工大学学报，2002，（1）．
[2]Eberhard P，Hüeber S，Yu J，et al．Multilevel numerical algorithms and experiments for contact dynamics[J]．Lecture Notes in Applied & Computational Mechanics，2006，（28）．
[3]胡爱萍，刘善淑，陈权．标准直齿圆柱齿轮传动接触强度计算的研究[J]．机械设计，2008，（11）．
[4]Hassan A R．Contact stress analysis of spur gear teeth pair[J]．World Academy of Science Engineering & Technology，2009，58（58）．
[5]魏延刚，管荣嵘．渐开线直齿圆柱齿轮啮合过程接触应力有限元分析[J]．大连交通大学学报，2009，（2）．
[6]宋新，陈计军．基于精确模型的渐开线齿轮齿根弯曲应力分析[J]．制造业自动化，2010，（3）．
[7]张秀华，李光喜，王婉．基于Ansys的渐开线直齿圆柱齿轮接触应力分析[J]．煤矿机械，2012，（2）．
[8]Pietrzyk K，Hagentoft C E．Probabilistic analysis of air in filtration in low-rise buildings[J]．Building and Environment，2008，43（4）．
[9]刘志全．航天器机械可靠性特征量裕度的概率设计方法[J]．中国空间科学技术，2007，（4）．
[10]Lü Q，Low B K．Probabilistic analysis of underground rock excavations using response surface method and SORM[J]．Computers and Geotechnics，2011，38（8）．
[11]戴鸿哲，王伟．结构可靠性分析的拟蒙特卡罗方法[J]．航空学报，2009，（4）．
[12]EEom Y S，Yoo K S，Park J Y．Reliability-based topology optimization using a standard response surface method for three- dimensional structures[J]．Structural and multidisciplinary optimization，2011，43（2）．
[13]费成巍，白广忱．航空发动机涡轮叶片径向变形的概率分析[J]．航空发动机，2012，38（1）．
[14]李昌，韩兴．基于响应面法齿轮啮合传动可靠性灵敏度分析[J]．航空动力学报，2011，26（3）．
