加法器是产生数的和的装置。加数和被加数为输入,和数与进位为输出的装置为半加器。若加数、被加数与低位的进位数为输入,而和数与进位为输出则为全加器。常用作计算机算术逻辑部件,执行逻辑操作、移位与指令调用。在电子学中,加法器是一种数位电路,其可进行数字的加法计算。本论文讨论的加法器均为全加器。
由于加法器在运算系统中的重要地位,诸多研究人员对于加法器做了许多深入的研究。文献[1]和文献[2]提出了低功耗低电压全加器的优化设计,并在降低功耗的基础上,提升了运算速度。文献[3]对加法器的逻辑特性进行了系统分析,为使用全加器的逻辑综合奠定了理论基础。
1 基础知识
加法器是产生数的和的装置。下文对几种简单加法器进行逻辑实现和逻辑分析。本节分析1比特加法器和2比特加法器的实现逻辑及所需的电路。
1.1 1比特加法器的实现及逻辑分析
设1比特加法器的两个输入分别为a、b,输出为cd,其中高位为c,低位为d。则1比特加法器的真值表见表1。
表1 1比特加法器的真值表
| a | b | cd |
| 0 | 0 | 00 |
| 0 | 1 | 01 |
| 1 | 0 | 01 |
| 1 | 1 | 10 |
由以上真值表可知,1比特加法器的逻辑表达式为:

经分析,1比特加法器需要1个异或门,1个与门,共2个逻辑门。
1.2 2比特加法器的实现及逻辑分析
2比特加法器的真值表见表2。
表2 2比特加法器的真值表
| ab | cd | efg |
| 00 | 00 | 000 |
| 00 | 01 | 001 |
| 00 | 10 | 010 |
| 00 | 11 | 011 |
| 01 | 00 | 001 |
| 01 | 01 | 010 |
| 01 | 10 | 011 |
| 01 | 11 | 100 |
| 10 | 00 | 010 |
| 10 | 01 | 011 |
| 10 | 10 | 100 |
| 10 | 11 | 101 |
| 11 | 00 | 011 |
| 11 | 01 | 100 |
| 11 | 10 | 101 |
| 11 | 11 | 110 |
其中,2比特加法器输入为ab、cd,输出为efg,低位为g,高位为f,进位为e。通过1.2的分析方法,由以上真值表可知:
g的逻辑表达式为:
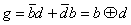
f的逻辑表达式为:![]()
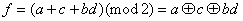
e的逻辑表达式为:
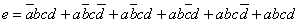
对e的逻辑进行化简可得:
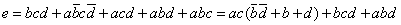 由对偶定理可得
由对偶定理可得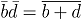 ,所以
,所以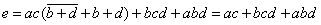 。
。
经分析,该逻辑需要5个与门和2个或门。
进一步整理,得:
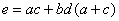
该逻辑需要3个与门和2个或门。
经统计与分析,2比特加法器需要3个异或门,3个与门和2个或门,共7个逻辑门。
2任意长度加法器的实现与逻辑分析
本节主要介绍通用任意长度加法器的设计方法,主要包括:①小长度加法器到大长度加法器的递推实现模型;②任意长度加法器的实现方法。
2.1 n比特加法器的递推实现模型
 2.2 任意长度加法器的实现方法
2.2 任意长度加法器的实现方法
结合1比特加法器和2.1介绍的递推实现模型,结合1比特和2比特加法器的实现逻辑,可以实现任意长度的加法器,实现逻辑如下:
(1)若N为偶数,可以将N比特加法器规约为![]() 比特加法器问题。
比特加法器问题。
(2)若N为奇数,可以将N比特加法器规约为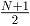 和
和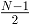 比特加法器问题。
比特加法器问题。
(3)以此类推,最终可以规约为1比特和2比特加法器问题。
2.3 实例
下面以6比特为例介绍加法器的实现过程。
所以,6比特加法器可以规约为3个3比特加法器问题。
3比特加法器的实现如下:
设3比特加法器的两个输入为A1A2;A3A4。
A1,A3为高位2比特,A2,A4为低位1比特。
A1与A3相加进位为e1;A2与A4相加进位为e2。
结合以上,由3比特加法器的实现方法以及1、2比特加法器的实现原理可得出每组3比特的实现原理
1比特加法器需要1个异或门,1个与门。2比特加法器需要3个异或门,3个与门和2个或门。3比特加法器可规约为2个2比特加法器和1个1比特加法器问题,则3比特加法器需要7个异或门,7个与门和4个或门。
经分析,6比特加法器需要21个异或门,21个与门和12个或门。
3 结论
本文经过对加法器基本原理的分析及对1、2比特加法器的逻辑实现和分析,推导出了用低位加法器实现高位加法器的递推实现模型,由此给出了任意长度通用加法器的实现方法。由于加法器是一种常用的、逻辑功能很强的中规模集成电路,因此对于加法器的逻辑设计所进行的讨论有助于进一步开拓加法器的应用领域。
参考文献
[1]卢君明,徐锋,胡鹏飞.低电压低功耗全加器的研究设计[J].固体电子学研究与进展,2004,4(3).
[2]张爱华,夏银水.面向低功耗的全加器优化设计[J].微电子学,2007,37(4).
[3]陈偕雄.使用全加器的逻辑设计技术[J].科技通报,1990,(1).
(徐州市第一中学)








