1 概述
1.1 红酒质量预测重要性
红酒,作为葡萄酒的一种,是经自然发酵酿造出的果酒。红酒中含有丰富的物质,其中葡萄汁含量最多占80%以上,酒精含量其次占10%~30%,还有酒石酸、果胶、矿物质和单宁酸和重要物质。这些物质共同作用,对酒质优劣起决定性作用,影响着红酒的品质。红酒是世界上最热销的酒水,不仅味道醇香诱人,营养价值也极高,对人体有诸多好处,既能预防疾病,也能美容养颜。随着我国社会的发展,物质文化生活水平也随之提高,饮用红酒的消费人群慢慢扩大,酿酒行业也发展十分迅速。红酒市场中的红酒种类繁多,且购买渠道多种多样,几乎随处可以买到红酒。但这个市场也是鱼龙混杂,好坏参半。目前,红酒市场里存有不少“假冒红酒”,这些看似光鲜的的红酒背后却是用化学原料的勾兑,运用色素、香精等辅料结合水、酒精在国内灌装和后变身原装进口酒。这不仅损害消费者的权益,更会对消费者的身体健康造成不利影响。因此,红酒的质量预测显得尤为重要。
1.2 红酒质量预测及其弊端
红酒质量预测不仅可以作为消费者购买的参考,还可以为红酒厂商提供建议,提升红酒的质量,促进红酒产业的发展。当前的红酒质量预测有许多种,应用感官品评技术评价酒体质量居多。与品酒师类似,运用感官和非感官的技巧来分析酒的原始条件以及酒的可能性变化,通过自身经验和客观独立的思考技巧来判断红酒质量。这种方法虽然比较简单,但受时间、人的精神以及味觉等外界影响,会对红酒质量的预测产生一定误差。而网上流行的鉴别方式也只是从红酒的单一或局部特点着手,从颜色气味或其他化学特性等方面预测质量,这些方式也具有一定的束缚性,不够严谨和科学。当下比较科学的预测方式为通过计算机进行预测,本文所介绍的预测方法为基于朴素贝叶斯原理的红酒预测。该方法利用机器学习对好的红酒各方面参数进行大量的分析,再结合朴素贝叶斯算法构建出模型,将其他红酒的数据输入模型中进行分析,即可得出结论,评判出红酒的好坏。
2 红酒质量预测系统介绍
2.1 机器学习概念介绍
机器学习是人工智能非常热门的一个方向,是实现人工智能的一种方法。机器学习顾名思义就是让机器可以像人一样去思考学习,它的基本算法是对现有的数据进行分析训练后可以预测和决策,对类似的问题或数据进行处理。机器学习的概念来自早期的人工智能研究者,已经研究出的算法包括决策树学习、归纳逻辑编程、增强学习和贝叶斯网络。本文所用到的是统计机器学习中的监督学习。
监督学习分为学习加预测两部分,主要步骤(图1)是:首先,搜集一个数据有限的训练数据集,将数据集分为学习数据和预测数据,其中利用学习数据构建模型,也称决策函数。然后,将预测数据输入到模型中,得到一系列结果,与原本得到的结果作对比,与原结果相同的越多,准确度越高,系统也就越好。
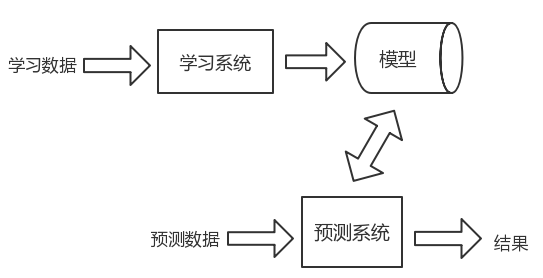
图1 机器学习预测过程
在监督学习中有两个误差概念,分别为训练误差和测试误差。通过训练数据集中的训练数据建立的模型,训练数据在该模型中计算产生的误差称为训练误差。而训练数据集中的测试数据在该模型中计算产生的误差称为测试误差。
监督学习中常出现的问题有欠拟合和过拟合。欠拟合是指通过较少的训练数据建立的简单模型,该模型不够拟合,产生的训练误差和测试误差较大。过拟合则相反,是在过量的训练数据下建立的模型,这样的模型一味追求对训练数据的预测能力,训练误差降低了,但往往不适用于新的数据,使测试误差升高。
监督学习可分为回归、分类两种。回归问题是将输入矢量和输出量用一个连续的函数连接起来,试图去预测一个连续值。分类问题是输入变量对应的输出变量为有限个离散值。
2.2 朴素贝叶斯算法训练机器学习模型(交叉验证)
贝叶斯分类是一系列分类的总称,这些算法均以贝叶斯定理为基础。而朴素又是独立的意思,故朴素贝叶斯算法是基于贝叶斯定理与特征条件独立假设的分类方法。这个在250多年前发明的算法,在信息领域有着无与伦比的地位。
朴素贝叶斯法其原理是根据某对象的先验概率和不同情况下的条件概率,计算出后验概率,然后选择最大后验概率作为结果。假设X是类标号未知的样本数据,H为某种假定,则P(H|X)为条件X下的H成立的后验概率。而现实场景中很多时候是无法直接通过统计得到P(H|X)的,贝叶斯法就可以由假设先验概率和在给定假设下通过观测数据得出的条件概率,得出一种计算方法:
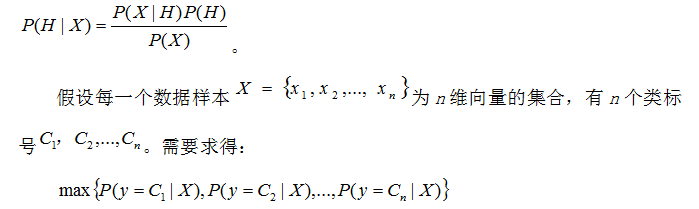
将分类问题转换为条件概率的问题,而P(X)对所有类都是常量,所以在X发生的条件下每个C分类出现的概率既P(C|X),然后取这个最大概率时的C就是我们的答案,确定为类标号![]() 。
。
因为X作为样本数据维度往往很大,如果任意特征组合在一起的概率全部考虑几乎统计不出来,这就要用到朴素贝叶斯的“朴素”二字。假设条件相互独立,求解的参数大大减少,只需单独求解一个P(X|C),然后相乘得:
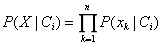
而先验概率可从训练样本中求得:
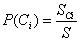
其中,分子是训练样本总数,分母是样本总数。
该算法的优点是模型比较简单,易实现且分类效果稳定;缺点也比较明显,在现实世界中的数据一般不满足条件独立性假设,且假设的概率分布可以有很多种,因此在某些方面会由于假设的先验分布的原因导致预测效果不佳。
2.3 使用训练集介绍
为了建立朴素贝叶斯算法模型和对红酒质量进行预测,通过对红酒质量的统计状况,建立训练数据集见表1。
表1 红酒质量预测的数据(部分)
| residual sugar | chlorides | free sulfur dioxide | total sulfur dioxide | density | pH | sulphates | alcohol | quality |
| 1.9 | 0.076 | 11 | 34 | 0.9978 | 3.51 | 0.56 | 9.4 | 5 |
| 2.6 | 0.098 | 25 | 67 | 0.9968 | 3.2 | 0.68 | 9.8 | 5 |
| 2.3 | 0.092 | 15 | 54 | 0.997 | 3.26 | 0.65 | 9.8 | 5 |
| 1.9 | 0.075 | 17 | 60 | 0.998 | 3.16 | 0.58 | 9.8 | 6 |
| 1.9 | 0.076 | 11 | 34 | 0.9978 | 3.51 | 0.56 | 9.4 | 5 |
| 1.8 | 0.075 | 13 | 40 | 0.9978 | 3.51 | 0.56 | 9.4 | 5 |
| 1.6 | 0.069 | 15 | 59 | 0.9964 | 3.3 | 0.46 | 9.4 | 5 |
| 1.2 | 0.065 | 15 | 21 | 0.9946 | 3.39 | 0.47 | 10 | 7 |
| 2 | 0.073 | 9 | 18 | 0.9968 | 3.36 | 0.57 | 9.5 | 7 |
| 6.1 | 0.071 | 17 | 102 | 0.9978 | 3.35 | 0.8 | 10.5 | 5 |
其中,数据集的前11项为X的各个属性,即对红酒质量预测的各个要素;最后1项为预测的结果即红酒质量。原本红酒质量应用3~8表示不同等级,而为了方便后面的模型运算和代码编辑,用0代表3、4、5,1代表6、7、8,既结果只有两种。
对于红酒质量预测数据集的使用是通过交叉验证的方法,将数据集分为训练集和预测集,大体按训练集70%,预测集30%的比例分配。
3 预测系统结果及改进
3.1 模型训练结果(使用交叉验证)
对系统结果进行预测要用到scikit-learn,也称sklearn。sklearn是Python下著名的机器学习库。sklearn里面有许多机器学习的算法,内涵大量数据集,是用来检验朴素贝叶斯算法的较好编程工具。首先,在sklearn中创建数据集,即将上面的数据导入sklearn中;随后,对数据进行预处理,将数据拆分成训练集和测试集,按照交叉验证将数据拆分为70%和30%;然后,在sklearn中定义模型,即朴素贝叶斯算法NB;最后,对模型评估,交叉验证得出结果如图2所示。

图2 朴素贝叶斯算法NB预测结果
最终,正确率较高,证明该算法是成功的。
3.2 系统改进
本模型采用离散分布,需要统计各个特性所出现的频率即条件概率的每一部分,一旦某一部分为0,则整个乘积为0,也会使后面的整个运算结果为0,影响分类的准确率。这时采用贝叶斯估计对先验概率的分子分母出现数都加1,样本数据够大不会对结果产生影响。对离散分布进行校准则不会出现0的情况。这称为拉普拉斯平滑,又称加一平滑。
另一种情况是容易出现下溢出。即概率往往非常小,一般为小数点后好几位,而条件概率使各个特征概率相乘四舍五入使乘积为零,造成下溢出。可以对乘积结果取自然对数,将乘法变为加法,通过求对数可以避免下溢出或者浮点数舍入导致的错误,如图3所示。
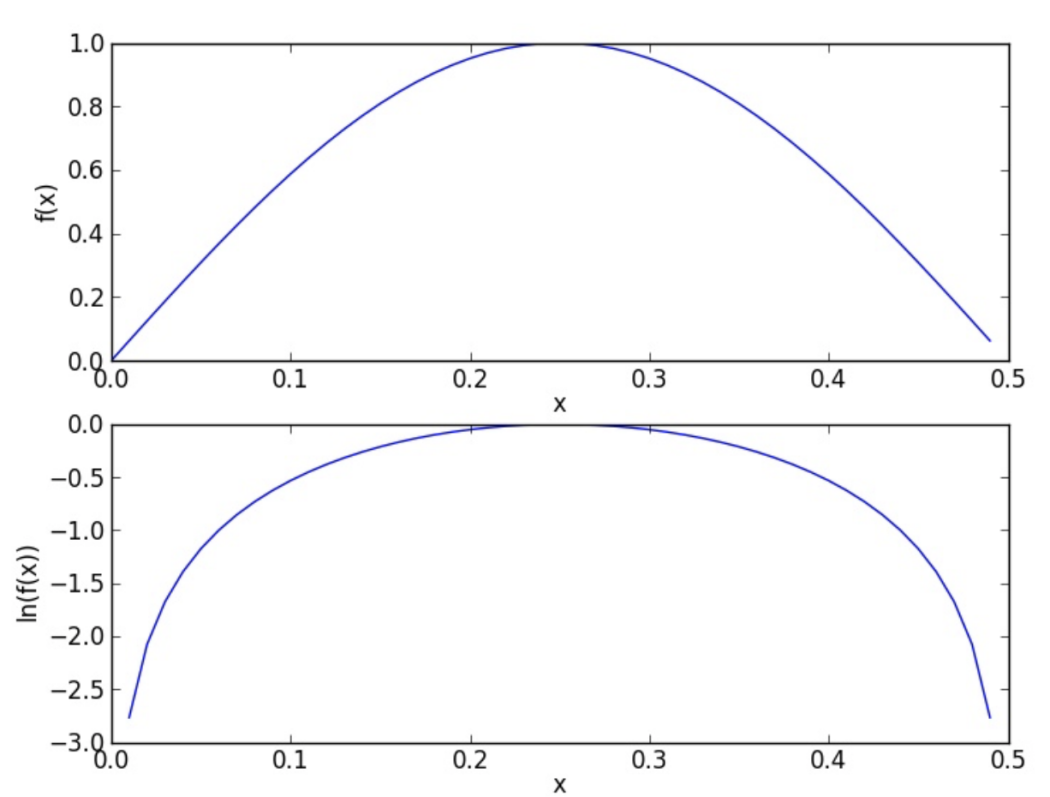
图3 函数f(x)和ln(f(x))的曲线
这样可以避免零的出现,且对数据不会有任何损失。
4 可实现的功能
红酒质量预测系统是在朴素贝叶斯原理下对机器学习的监督学习的应用。该系统的建立首先需要搜集一个含大量有效数据的数据集,包含在不同酒精含量(酒精度)、酸度和糖分指标以及pH下红酒质量的评估数据,将这个数据集分为训练集和预测集,通过前者构建想要的模型,后者用来检验模型准确性。而模型的建立需要运用一种常用贝叶斯运算法:
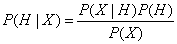
结合该系统应为在相同因素的不同情况下影响红酒质量好坏的概率。模型准确性的检验要用到sklean编程通过前面运用交叉验证分的数据集对模型进行检验,模型通过训练集的学习利用预测集的数据进行红酒质量预测,得到红酒质量与预测集本知道的红酒质量进行对比,正确率高说明系统模型准确性良好,也证明系统是可运行的,可以利用这个系统根据红酒质量的影响因素综合分析得出红酒质量好坏,对酿酒和红酒选购有很大帮助。
5 结语
本文基于机器学习和贝叶斯算法提出一种朴素贝叶斯原理的红酒质量预测系统,在一定小的错误率下通过对数据集的处理和代码验证情况,系统运行状况良好,证明了朴素贝叶斯算法在实际应用中的实用性,实现了科技与生活的融合。朴素贝叶斯算法基本可以用来对市场上的红酒质量进行预测,为红酒质量预测提供了一种新方法。在今后要继续对朴素贝叶斯系统进行改良,不断进步,力求找到更加准确、简便的预测方法。
参考文献
[1]余芳,姜云飞.一种基于朴素贝叶斯分类的特征选择方法[J].中山大学学报(自然科学版),2004(5):118-120.
[2]李静梅,孙丽华,张巧荣,等.一种文本处理中的朴素贝叶斯分类器[J].哈尔滨工程大学学报,2003(1):71-74.
[3]陈欣.葡萄酒的质量预测模型[J].西安文理学院学报(自然科学版),2013,16(2):45-47.
[4]刘瑜.基于葡萄酒品基础数据的综合分析系统设计与实现[D].济南:山东大学,2013.
(山东省淄博第四中学)








