1 多维度合并测评的基础：主成分分析法
当前学术界普遍认为，主成分分析法具有科学、客观地将一个多目标问题整合成一个单指标形式，客观地确定多个指标的权重的优势。本文运用该方法对地方领导力强度进行分维度的指标权重确定，并在此基础上，整合六个维度得到总体的地方领导力强度数值。用公式简明表述如下：
F地方领导力强度=F经济推动力+F产业结构转型力+F自主创新力+F生态保护力+F公共服务力+F社会保障力
式中，F地方领导力强度为地方领导力强度值；F经济推动力为经济推动力值；F产业结构转型力为产业结构转型力值；F自主创新力为自主创新力值；F生态保护力为生态保护力值；F公共服务力为公共服务力值；F社会保障力为社会保障力值。
1.1 数学原理
本次使用主成分分析法，主要是将以往原有指标进行重新组合，获得一组的互相无关综合指标后，以地方领导力强度测评为依据，选择数量较简洁的综合指标，保证原有指标的信息的有效反应。
A×b阶的指标数据矩阵
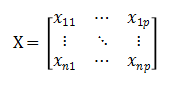
式中，a为指标数量；b为指标变量；X的第i个列向量最终量为b；而数据矩阵X的b个向量（即b个指标向量）（即综合指标向量）为：
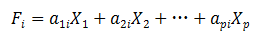（i=1，2，…，b）
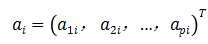
这种情况下从原有指标所提供的信息总量中，b个主成分所提取的信息量呈现依次递减情况。而使用方差可对每一个主成分所提取的信息量进行细化描述，其中主成分方差的贡献率为：原指标相关矩阵相应的特征值，而每一个组合系数与特征值的特征向量具有一致性，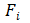
的方差贡献率的大小与相应主成分反映综合信息的能力成正相关。
1.2 计算步骤
本文依据傅湘和纪昌明（1999）构建区域水资源承载能力综合评价体系中的计算步骤，对地方领导力强度测评体系中的原有指标进行了预处理。
2 确定权重的基础
2.1 数学原理
在统计学中，依据信息熵的定义，评价矩阵Y中第i项指标的信息熵为：
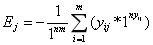
当某指标对研究对象作用的概率相等时，为信息熵值最大值1。基于等概率作用的相关内容，该指标包含的信息量对相关研究对象具有同等效用，其对最终评价结果无影响。这种情况下，某项指标的信息效用价值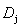
就主要由该指标的信息熵决定，即某指标信息效用价值为
。
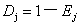某一指标的效用价值与其对评价的重要性、权重成正相关，因此某项指标熵权为：
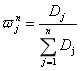
式中，i为指标项数；D为指标信用价值。
2.2 计算步骤
2.2.1 对数据进行标准化处理
地方领导力强度指标体系的数据分为正向指标和负向指标两种。假设评价指标j的理想值为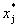
，正向指标是指
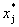越大越好的正向计分指标，记为
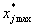。负向指标是指
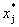越小越好的负向计分指标，记为
。
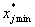正向指标数据标准化处理公式为：
2.2.2 指标信息熵值E和信息效用值D
第j项指标信息熵公式如下：
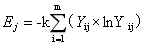
式中，K为常数；m为样本数量；k与m具有适当比例关系，即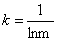
。
2.2.3 单评价指标权重核算
熵值法利用该指标信息的价值系数来计算个指标的权重分布，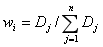
。价值系数越高，对评价的重要性就越大。
2.2.4 指标评价得分
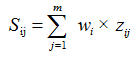
式中，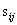
为第i个年份第j项评价指标的数值；m为评价年数；n为指标数。
3 相对效率评价方法：DEA模型
领导力强度测评能摒弃地域因素对不同省长及其领导班子的影响，是一个相对的概念。因此，在对领导力强度进行分维度测量时，应优选相对效率评价方法进行数据加工处理。
3.1 传统DEA效率评价模型的数学原理
当效率概念应用于某一组织的绩效评价的时候，多研究该组织在消费一定的生产资源时最佳生产率或者最小的成本控制可保证成本最小化。这两种观点分别是从产出和投入视角对“相对效率”进行的评价。
DEA主要以包络线的概念对一般微观经济学中的生产函数进行了综合分析。以DEA模式的概念评价各地省级政府领导班子和领导干部的领导力强度这一相对概念，可以确定有效率、无效率的决策单元特点，即有效率的决策单元主要为效率前言构成部分，而无效率的决策单元主要对效率前沿相对位置确定进行无效率程度评估。当效率值界定为1时可将决策单元数值生产前沿，而决策单元数值低于生产前沿则认为DEA无效。一般这一数值介于0～1之间。因此，效率是一组没有绝对大小的相对指标。本文只能比较同一年度各地领导力强度之间的效率，而不能比较各地不同年度的领导力强度。
Farrell（1957）提出的效率衡量模型描述了DEA模型度量相对效率的数学原理和步骤。在决策单元数量一定的情况下，每个决策单元投入要素、类型的产出要素具有一定的比例关系，将全部投入要素、产出要素进行整合，可对整体投入产出指标集进行确定。在规模收益一定的情况下，某个决策单元的相对效率求解过程是：
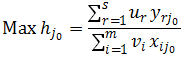
约束条件是：
3.2 基于Malmquist指数方法的DEA模型原理
Malmquist生产率指数是基于DEA模型的方法提出的，具体原理如下：
上述例子主要对变动规模报酬的情形进行了分析，即在分解技术效率的情况下，分别对纯技术效率、规模效率变化情况进行分析。本文运用此方法，将中国地方领导强度测评中生态保护力与自主创新能力的生产率变化分为技术变化、技术效率变化两个方面。技术效率变化主要为纯技术效率、规模效率两个方面。结合实证分析对纯技术效率、规模效率对技术效率变化的影响，可逐步确定相关区域内相对效率发展趋势。
4 结语
综上所述，地方领导力强度评测逐渐取代传统政绩考核评价，可以准确地评测地方官员在促进地方区域科学发展水平的贡献程度。常用的地方领导力强度评测方法包括主成分分析法、熵值法、相对效率评价法等，通过对上述方法的特征和要点进行分析，能够显著提高评测结果的真实性和准确性。
参考文献
[1]傅湘，纪昌明．区域水资源承载能力综合评价——主成分分析法的应用[J]．长江流域资源与环境，1999，（8）.
[2]孙刘平，钱吴永．基于主成分分析法的综合评价方法的改进[J]．数学的实践与认识，2009，（9）.
[3]傅湘，纪昌明．区域水资源承载能力综合评价——主成分分析法的应用[J]．长江流域资源与环境，1999，（8）.
[4]马文明．基于主成分分析法和熵值法的我国指数基金综合评价[D]．长沙：中南大学，2007.
[5]余燕．新疆城乡一体化发展的水平和效率分析——基于熵值法和数据包络法[J]．广西职业技术学院学报，2016，（8）.
[6]张卫民．基于熵值法的城市可持续发展评价模型[J]．厦门大学学报，2004，（2）.
[7]Farrell M．The Measurement of Producitve Efficiency[J]．Journal of the Royal Statistical Society，1957，（120）.
[8]张宝．中国信托公司效率及全要素生产率的测度与影响因素研究[D]．长沙：湖南大学，2012.
[9]维权龄．数据包括分析[M]．北京：科学出版社，2004.
[10]刘秉镰，李清彬．中国城市全要素生产率的动态实证分析：1996—2006——基于DEA模型的Malmquist指数方法[J]．南开经济研究，2009，（3）.
（作者系清华大学公共管理学院副研究员，博士）
