传统的船舶结构分析所采用的计算参数是一些确定的数值,往往忽略了实际结构分析中荷载、材料性能、几何尺寸以及结构的变异性等种种不确定因素的影响,而采取安全系数法对结构进行强度储备,带有较强的主观性,经济性也不够理想。游艇的艇底骨架和舷侧等结构承力较大,且各结构部位所承受外载荷和结构的构造本身都具有很大的不确定性,传统的安全性校核方法不能很好的反映出游艇在遭遇不确定性外载荷的情况下的安全系数,而需要基于结构可靠性的原理对其进行分析,从而确定游艇的艇体在极限承载能力下的安全余量。游艇的艇体结构强度可靠性分析需要结合游艇所受的外载荷、极限承受强度以及可靠性的计算方法。本文根据游艇总纵弯矩下的可靠度计算模型,通过一次二阶矩法对一艘78ft的游艇进行艇体的结构可靠度计算。
1 游艇总纵弯矩下的可靠度计算模型
本文在进行游艇艇体的可靠性分析时,取结构的最大应力点的应力值作为结构的极限承载能力,计算游艇艇体结构在外载荷作用下达到或超过这种极限状态的概率。根据对游艇的极限状态受力分析可得,总纵弯曲下游艇所受外载荷为静水载荷和波浪载荷的和,则可靠度计算模型为:

2 可靠性计算方法

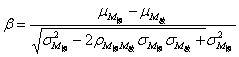 (6)
(6)
3 算例分析
对一艘78ft游艇进行关键部位结构可靠性计算,其主要参数见表1。
表1 游艇的主要参数
| 参数(单位) | 数值 |
| 总长(m) | 23.91 |
| 垂线间长(m) | 19.19 |
| 船宽(m) | 5.99 |
| 水线宽(m) | 5.16 |
| 排水质量(t) | 60 |
| 最大航速(kn) | 31 |
| 设计吃水(m) | 1.111 |
| 最大吃水(m) | 1.187 |
| 最大倾斜角(deg) | 17.73 |
根据游艇艇体结构的有限元计算结果,可以得出游艇总纵弯矩随波浪频率变化图,如图1所示。
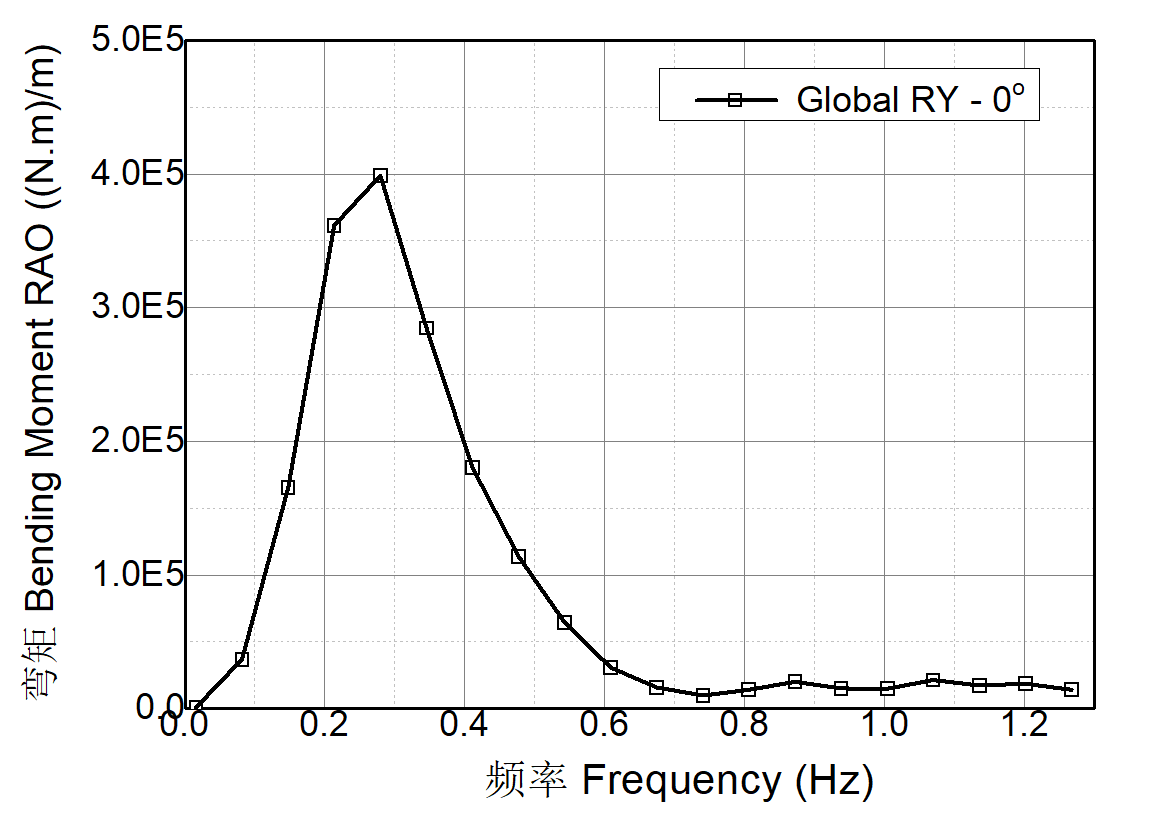
图1 总纵弯矩随波浪频率的关系曲线
总纵弯矩分为中拱和中垂两种情况,用中拱和中垂两种状况下的波幅分别乘以图1曲线纵坐标峰值,可得出在中拱和中垂状态下的艇体极限弯矩分别为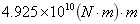 和
和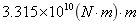 。
。
Maxsurf计算结果见表2。
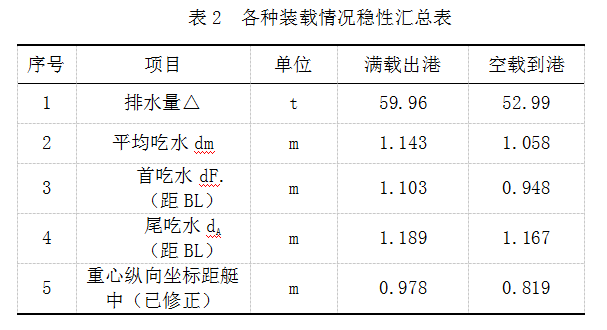

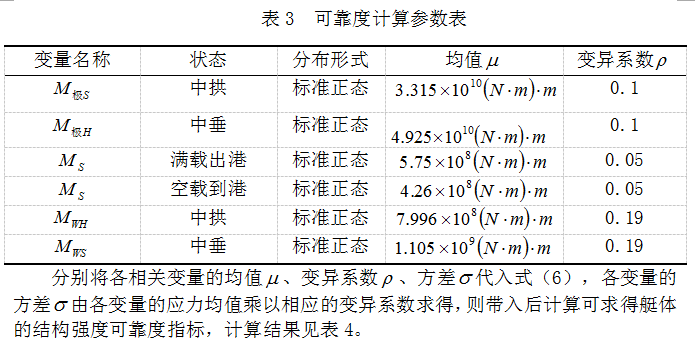

计算结果表明,游艇艇体在两种载况下均具有良好的可靠性指标,而中垂状态下游艇艇体的可靠性指标明显偏低,根据梁弯曲理论,最危险的位置是艇中剖面艇底处。因此,可将中垂状况下的空载到港艇底可靠度指标作为整个艇体的可靠度。
4 结语
本文在参考相关文献的基础上,通过一次二阶矩法,对游艇在满载出港和空载到港两种载况下的艇体结构强度可靠度进行了计算,得到了艇体结构的可靠性指标。计算结果表明,两种载况下游艇艇体结构的失效概率均小于![]() ,即可靠性指标均大于3.719,符合可靠度要求。
,即可靠性指标均大于3.719,符合可靠度要求。
参考文献
[1]黄树煌,林少芬.船舶总纵极限强度可靠性分析[J].舰船科学技术,2011,33(10).
[2]李杨梅.玻璃钢游艇总纵弯曲下的结构可靠度计算[D].厦门:集美大学,2015.
[3]胡健康,林少芬.船舶横稳性可靠性分析研究[C].全国机械行业可靠性技术学术交流会,2014.
[4]张明,金峰.结构可靠度计算[M].北京:科学出版社,2015.
[5]朱静,郭军.复合材料船体结构可靠性分析[J].中国造船,1996,11(135).
(作者系集美大学轮机工程学院硕士研究生)








