0 引言
高刚度、高强度的航空复合材料夹层梁结构近年来被广泛应用于飞机结构。大部分研究夹层梁结构优化时所针对的载荷情况均为3点弯曲，其目的要么侧重于重量最小化，要么侧重于材料选择。这些研究中大部分定义了两个设计变量：芯层厚度，面板厚度；一种约束条件：刚度约束或强度约束。本文用3个设计变量（芯层厚度、面板厚度、泡沫相对密度）研究刚度和强度共同约束下的夹层梁的优化，分析均布载荷下夹层梁的失效模式并寻求有效的强度、刚度约束组合，并求解出最优设计变量组合，以期达到重量最小。
1 夹层梁模型
为了简化计算，夹层梁两边的悬臂长度忽略不计。均布载荷w作用在梁的上表面。梁的下表面有两个支撑点。梁的宽度（垂直于纸面方向）b，长度L，面板厚度t，芯层厚度为c，上下面板形心间距为d=c+t。假设芯层的厚度c远大于面板厚度t，从而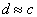
，对应的无量纲化设计变量为芯层相对厚度
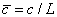、面板相对厚度
。
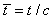2 材料性能
本文研究的夹层梁模型由复合材料面板和泡沫芯层组合，其材料性能参数见表1。
表1 夹层梁的材料性能参数
3 强度
3.1 失效模式
在均布载荷下，复合材料夹层梁结构共有四种失效模式：芯层剪切（core shearing）、面板委屈曲（face microbuckling）、局部压陷（local indentation）、压塌（core crush）。在均布载荷下，由于载荷在上表面分布均匀，不存在面板微褶皱的情况。通常，夹层梁的强度取决于最弱的失效模式。
3.2 强度表达式
3.2.1 芯层剪切失效模式下的强度表达式
在夹层梁的柔性刚度分配中，芯层的作用微乎其微，因此可以假定在整个芯层深度范围内，剪切应力的大小保持不变。
定义无量纲化的压强（均布载荷）指数：
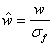（3）
对于芯层剪切，有：
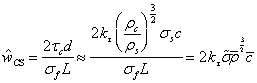（4）
3.2.2 面板微屈曲失效模式下的强度表达式
面板受压时，如果沿轴向的应力达到面板的微屈曲强度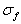
，复合材料面板就会发生微屈曲现象。定义无量纲化压强指数为：
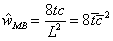（5）
3.2.3 压陷失效模式下的强度表达式
本文只探讨纯弹性芯层情况下的压陷模型。定义无量纲的压强指数为：
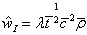（6）
其中：
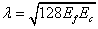（7）
3.2.4 芯层压塌失效模式下的强度表达式
当芯层内的压力达到芯层的抗压强度时，芯层会发生压塌现象，有：
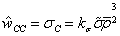（8）
4 优化
4.1 优化目标
优化的目标为特定性能要求下将夹层梁的重量（或质量）最小化，如满足刚度约束或满足强度约束条件下。夹层梁的质量M，由芯层的质量和上下面板的质量两部分组成。定义一个无量纲化的质量指数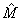
：
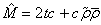（9）
本文只关心强度约束条件下的优化以及刚度和强度共同约束条件下的优化，同时引入“活跃”约束条件和“不活跃”约束条件的概念。对于强度约束，活跃的约束是指，当相应的载荷加到梁上时梁会出现相应的机理或表现；即，载荷的微小增量都将导致机理失效。对于刚度约束，活跃的约束是指，在组合的设计变量下，梁刚好能满足刚度要求；即，如果刚度需求稍高一些，现有几何尺寸就无法满足。不活跃的约束则恰好相反，对强度而言，如果约束是不活跃的，则如果载荷稍微增加一点，梁的相应机理也不会失效。对刚度而言，如果约束是不活跃的，则梁的刚度稍微增加一点，梁的刚度约束条件也能满足。
4.2 优化方法
在3个设计变量条件下，Kuhn-Tucker条件不再有效，由此提出一个新的想法以获得最优设计变量，即：如果两种失效模式同时发生，利用失效机理的定义，从
的表达式中消去两个变量，即把其中两个变量表示为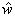
和第三变量的函数，随后把这两个变量代入
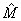的表达式后对第三变量求偏导，即可获得第三变量的极值（即最优值）。重新选择第三变量，即可获得另外两个变量的极值。如果3种及3种以上失效模式同时发生，则可以从3个或4个
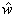表达式的方程组中直接求解。此唯一解却不一定是最优解。
4.3 失效图
本文采用的实效图是一种简化的实效图，即将泡沫相对密度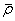
设定为常数，从而在
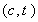的二维坐标系下画失效图。这个二维失效图可以看作是三维设计空间
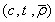中的一个截面。
如图1所示，图中的5条不同颜色的曲线分别代表四种失效模式之间的边界方程（I代表indentation，MB代表Micro Buckling，CS代表Core shearing，CC代表Core Crush）。联立相应公式求解可得相应的边界方程，由图中可以看出压陷失效模式与压塌失效模式之间并没有合理的边界方程。
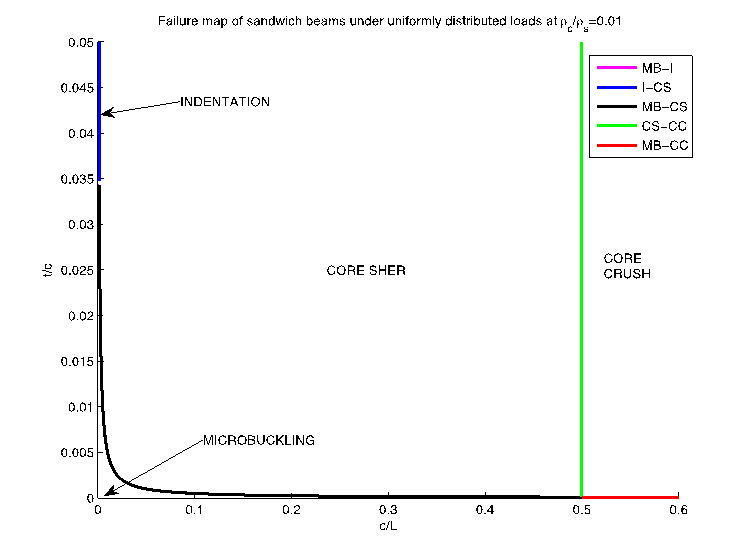
图1 均布载荷下夹层梁结构的失效图
从上图可以看出，均布载荷下夹层梁结构的主要失效模式为芯层剪切，几乎占据了整张失效图，而剩下部分则主要由面板微屈曲失效模式占据；可以忽略压陷失效模式，因为它只占据极小的一篇领域；同样可以忽略压塌失效模式，因为它只当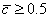
时发生，而此时的设计变量是不切实际的。
4.4 结果与分析
文中示例梁长度1m，宽度0.1m，需承受最大为1kN的载荷，最大变形量为10mm。其结构为聚合为泡沫芯层和玻璃纤维复合材料面板。相应的压强指数为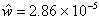
，其他参数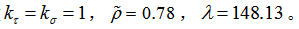
。
在强度和刚度组合约束条件下，均布载荷下夹层梁结构一共有26种约束组合。其中，只有3种组合是合理的。本节以组合（2）为例进行失效图分析。
5.4.1 面板微屈曲强度约束、芯层剪切强度约束共同作用
根据5.2节部分的优化方法，当面板微屈曲和芯层剪切失效模式同时活跃时，可以得到相应的最佳设计变量组合。
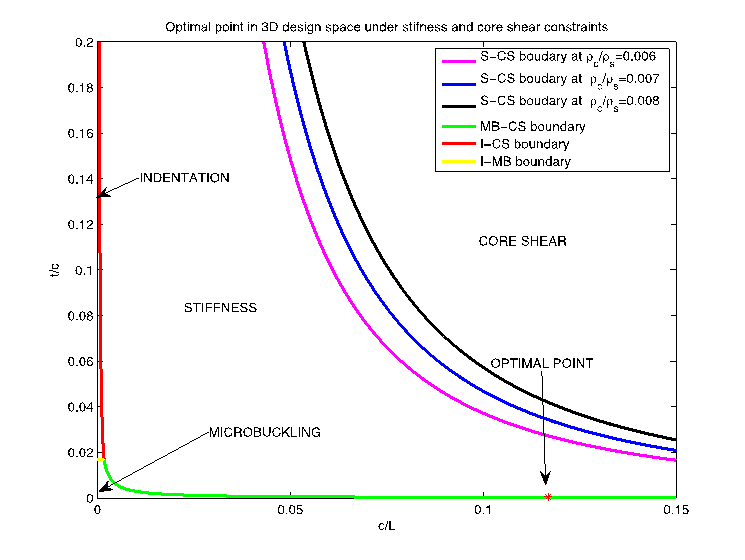
（a）三维空间内刚度约束和芯层剪切强度约束条件共同作用下的最优设计点
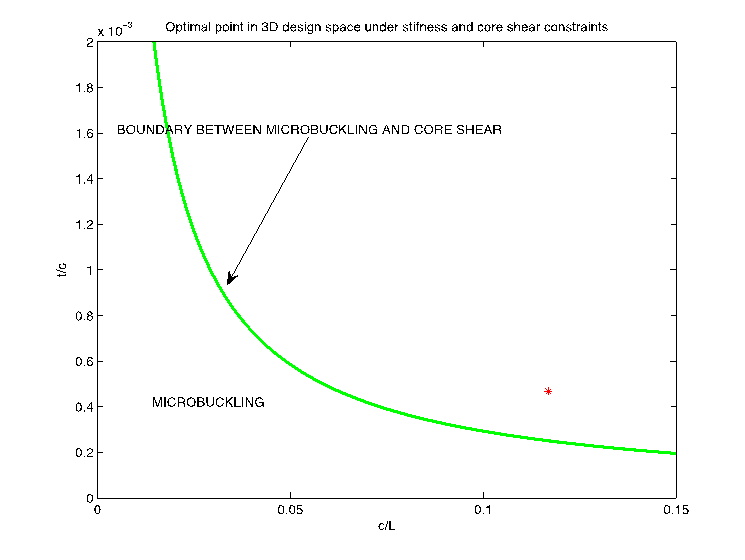
（b）图a的下半部分（局部放大）
图2
4.4.3 刚度、面板微屈曲强度约束、芯层剪切强度约束共同作用
这3种约束同时满足时，求解如下：
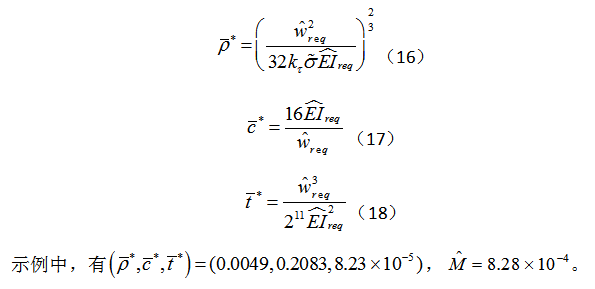
5 结语
本文得出了均布载荷下夹层梁结构在强度单独约束、强度和刚度组合约束下的最优设计变量组合解，并通过失效图分析验证了各种组合解的合理性。需要指出的是，在示例梁中，在增加了刚度约束条件后，最小质量会略有增加。比较组合解（1）和组合解（3），质量指数增加了2.1%，刚度指数上，后者是前者的3倍左右。因此，这种方法是合理的。
（作者系中国商用飞机有限责任公司美国有限公司项目经理，助理工程师，）
