1 地心坐标系取代参心坐标系的必要性
1954年北京坐标系源自前苏联克拉索夫斯基椭球,其与中国似大地水准面吻合度较差故后建立西安80坐标系。西安80坐标系的建立方法仍为传统方法,其应用中常涉及到变形问题,会附带出现变换投影面、偏移中央子午线、椭球平移、椭球膨胀等一些列抵触投影变形的方法,随之产生了各类地方坐标系(或独立坐标系)。这为数据的统一应用、地球模型的精化等带来不利,也会在个别地区积累较大的误差而无法消除。而在现有科技条件下、国民经济支持下所建立的国家2000大地坐标系将能更好地服务于科学技术、国防安全、社会生活等各个层面,为测绘人员提供更趋完善、精密、合理的测量坐标系统。
2 参心坐标系向地心坐标系转换实质
参心坐标系向地心坐标系转换实质上属于不同参考椭球间的转换。常用的转换方法有布尔沙模型、范士模型和莫洛琴斯基模型等。国际上比较常用且模型相对完善、精度已得到学术界和应用界普遍认可的是布尔沙模型(七参数模型)。
2.1 布尔沙模型
布尔沙模型全称为布尔沙-沃尔夫(Bursa-Wolf)模型。该模型采用了含有7个参数的矩阵模型,利用最小二乘原理来求解椭球间的转换关系,其中含有平移参数3个、旋转参数(欧拉角参数)3个和尺度变换参数1个。具体转换模型如公式(1)所示。
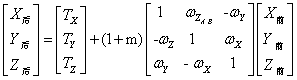 …(1)
…(1)
式中,TX、TY、TY为各分量平移参数,ωX、ωY、ωZ为各分量旋转参数,m为尺度比参数。由公式(1)可以明显看出:TX、TY、TY、ωX、ωY、ωZ和m这7个未知参量是所需要的7个参数,在实际工作中只要求解出这7个参数就可以解决椭球间的坐标转换问题。
根据公式(1)还可以看出:需要有3对以上的同名公共点(具备两套椭球的坐标)才可以求解出对应的7个参数。所以具备3对以上满足精度的公共点是布尔沙模型实践过程中的必要条件。
2.2 地图投影的影响
众所周知,地球是一个不可以延展为平面的不规则近梨形体;即使在地球模型建立时将其模拟为一个规则的椭球体,但该椭球体依然是一个不可充分延展的形体(个别地区精度难以满足)。
传统的地图投影理论将测量边长、椭球面和坐标系的关系具体表现为:地球表面——参考椭球面——高斯面的二次投影。
由于传统地图投影方法必然产生不同程度的投影变形(或角度、或长度、或角度和边长共同变形),我国通用的高斯-克吕格投影本质是等角投影,虽保证了角度的不变但却带来了长度的变形,在实际工程应用过程中一般是利用两次变形符号相反的特性,偏移子午线和改变投影高来解决精度问题(或同时改变这两个因素)。
根据资料显示:国家原有大地控制网(GPS)与国家天文网归算到同一坐标系时,发现天文大地网存在局部的伸缩、变形及扭曲。GPS网点与天文网点有14条弦长中误差超过1m,最大的达到3.77m。
所以,旧有参心坐标系的建立细节和现存精度等都会影响到其向地心坐标系的转换精度,应当引起从业人员的高度重视。
3 坐标转换实例应用
3.1 项目概况
应吉林省某县农村集体建设用地和宅基地确权登记发证项目需要,需在原有C级GPS(西安80坐标系)基础上加密D级控制网点并联测国家2000大地坐标系得到各点在国家2000大地坐标系下的坐标以及转换关系。
该县位于吉林省西部,东接农安县,南邻公主岭市、双辽市,西毗连科尔沁左翼中旗,北通通榆、乾安、前郭尔罗斯县。县辖面积5736.3064km²,东经123°06′~124°45′,北纬43°59′~44°42′。
经多方渠道共收集到1980西安坐标成果C级GPS控制点18个,国家2000大地坐标系C级GPS控制点21个,公共点14个。
3.2 旧有椭球坐标系的分析与处理
依据甲方提出的控制网精度要求,其精度必须达到工程测量中不大于2.5cm/km的要求,同时满足不得将乡(镇)分割在不同的投影带。因此首先要进行旧有西安80坐标系的精度分析及处理。
依据建立的平面直角坐标系进行理论分析,采用排除法进行筛选,最终确定建立任意带平面直角坐标系(任意带西安80坐标系)可对投影进行抵偿而达到控制网精度要求。具体参数如下。
平面坐标系统:高斯-克吕格任意带分带投影平面直角坐标系;
投影:高斯—克吕格任意带分带投影;
中央子午线分别为123º30′、124º30′;
高程抵偿面:采用150m平均高程面;
大地基准:采用1980西安坐标系参椭球元素值。(长半轴a=6378140±5m、扁率α=1/298.257)
3.3 任意带投影坐标精度验证
验证精度时选取了能够覆盖全县范围的D级网上的基线边长共计20条,首先将解算出来的基线边长利用两端点的高程进行改平计算,得到基线水平边长,再用端点坐标反算边长进行比较,得到每公里的变形量。
西区(中央子午线 123º30′)投影变形最大为1.29cm/km,分布在测区的东部边缘;投影变形最小为0.08cm/km,分布在测区的中部偏东侧;一般变形为0.33cm/km。东区(中央子午线124º30′)投影变形最大为1.85cm/km,分布在测区的西部边缘;投影变形最小为0.13cm/km,分布在测区的中部偏西侧;一般变形为1.15cm/km。整个测区边长投影变形值均小于2.5cm/km,满足设计要求。
就此,新建立的基于1980西安坐标系参椭球的任意带独立坐标系的精度足以满足该工程的需求及与国家2000大地坐标系的转换精度。
3.4 国家2000坐标系精度及坐标转换
3.4.1 国家2000坐标系的内符合精度
根据现有21个国家2000坐标系控制点分析结合JL-CORS数据,可知该21个点满足精度要求,其长度变形量在0.47~1.23cm/km,高程(国家2000大地高)精度在1.20~2.11cm之间。因此,完全满足本工程坐标系转换的要求。
3.4.2 任意带80系向国家2000系转换
分析:因该21个点中只有14个公共点,将其与新建立的任意带西安80系进行网间匹配,发现有3个点的匹配度大于3cm,故将其剔除,使用11个点进行椭球间的转换。其中西区(中央子午线为123º30′的区域)有5个公共点,东区(中央子午线为124º30′的区域)有6个公共点。转换后的精度如表1~表2所示。
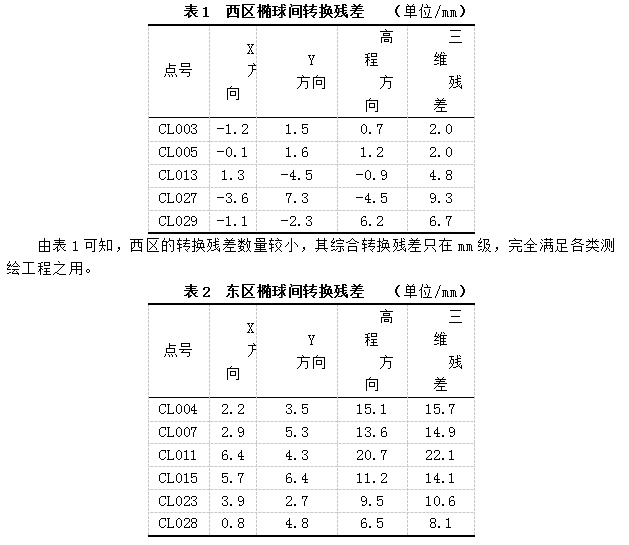
由表2可知,东区的转换残差在数值上较西区略大,其综合转换残差能够达到cm级(最大2.2cm),满足该工程使用。
3.4.3 转换成果的验证
根据东、西两区域内收集到的可利用的11个含有西安80坐标系和国家2000坐标系成果的坐标数据求得了东、西两区域的两套七参数。
根据该两套七参数和转换软件,求取了各区未知C级网点的国家2000坐标系坐标(包含原有3个精度稍差的控制点的坐标改正)及新布设全部D级控制网点的国家2000坐标系坐标。就此,该工程所得到的测绘成果即可以在西安80坐标系和国家2000坐标系下实现实时、高精度转换。
为保证成果的可靠性,在测区内选取布设的20个控制点进行快速静态的复测,东、西两区域各复测10个点,以分部均匀的4个控制点为起算进行平差,求取各自区域内6个点的国家2000坐标系坐标与软件转换的坐标进行对比。具体数据见表3。
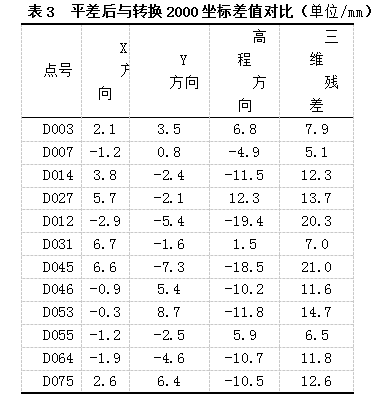
由表3可看出:其转换平面精度可达到mm级(最大9.8mm),其转换高程精度可到达<2cm级,其三维精度可达到2cm左右。故而转换后的国家2000坐标系坐标精度完全满足设计要求。
4 结论与展望
4.1 原有控制网分析至关重要
椭球间转换是旧椭球向新椭球转换,而一般情况下旧椭球采用传统参心坐标系建立,需进行必要的控制网精度分析。只有旧椭球坐标系控制网的内符合精度合格才是进行转换的基础,否则转换工作无从谈起。
如旧有椭球通过投影得到的旧有坐标系变形率不足以满足工程需要,需采取适合的方法建立旧有椭球下的满足精度的独立坐标系统(如本文),只有坐标系统内符合精度满足要求才能继续进行其到新椭球的坐标转换。
4.2 新椭球下控制网精度应可靠
与上节同理,虽然新椭球控制网建立较晚,等级较高,选点、地质条件等都较合理,但随着时间的推移、地壳活动、地质结构变化、其他外力影响等因素,会导致个别点可能出现破坏或扰动而无法达到原有的精度要求。
故而,检查新椭球坐标系统控制网的内符合精度十分必要,新椭球坐标系下网内符合度也是制约转换精度的重要因素。
利用已有精度合格的点,剔除、改化精度不能满足要求的点是对新椭球坐标系统下坐标转换用控制点选取的原则。
4.3 有效利用其他资料
如果能收集到高精度的WGS84经纬度、高精度的国家2000大地坐标系经纬度、高精度似大地水准面模型、连续运行参考站相关数据等将会为坐标转换工作提供更多便利。
4.4 展望
随着地球物理学发展、地球理论模型的深入研究和方法的逐渐优化,将会有操作更加简便、精度更高、试用范围更广的坐标系统转换方法诞生。
随着国家2000大地坐标系的广泛使用,其自身诸多的技术优点、精度优势等逐渐显现;而在其完成跨省无缝连接后,必将更加有效地在国民经济相关领域发挥不可或缺的作用。
参考文献
[1]徐绍铨,张华海,等.GPS测量原理及应用(第四版)[M].武汉:武汉大学出版社,2017.
[2]张显云,杜宁,张俊.GPS技术建立地方独立坐标系的方法分析[J].矿冶工程,2012,32(5):23-25.
[3]李玉宝,沈学标,等.控制测量学[M].南京:东南大学社,2013.
[4]孙达,蒲英霞,等.地图投影[M].南京:南京大学出版社,2012.
收稿日期:2018-11-12
作者简介:王百胜(1986-),男,辽宁阜新人,21092119860303301X,工程师,研究方向:公路、铁路和港口等施工工作。








