1 引言
随着捕捞强度逐渐增加,海洋污染范围不断扩大,在世界范围内海洋渔业资源的衰退现象日益严重。海水养殖业作为对海洋捕捞的补充,近年来得到了快速发展。但海水养殖带来的环境、病害及质量安全问题也渐渐显露出来。深海养殖与加工基地的研究、开发和应用已成为主要海洋国家的战略选择。开展深海养殖与加工基地建设,一方面能够提高某些经济品种的产量或整个海域的鱼类产量,以确保水产资源稳定和持续的增长;另一方面在利用海洋资源的同时重点保护海洋生态系统,实现可持续生态渔业。
深海养殖与加工基地总体规划是基地建设的核心问题。然而,运行环境是复杂的、多变的,影响未来航运市场状态的因素是众多的,在这种情况下要进行准确的预测是非常困难的。进行深海养殖与加工基地规划主要有两种办法:一是凭个人经验,二是借助于数学规划方法。
本文基于组合优化方法,研究深海养殖与加工基地的规划论证,以四年总营运成本现值最小作为目标函数,建立规划模型,根据分析实际情况建立约束条件,提出相应的规划方案。
2 论证方法
2.1 船队规划方法的研究现状
现阶段的船舶数学规划方法主要有线性规划、整数规划、动态规划等方法。
(1)线性规划方法数学模型和解法具有通用性、求解速度快、使用方便等特点。同时,线性规划方法的数学模型也有求解出来的决策变量(船舶艘数)一般不为整数,需要人工圆整为整数等不便。
(2)整数规划方法,可以弥补线性规划的决策变量不为整数的不足,但也给模型的求解带来不便。而整数规划模型又可分为纯整数规划模型、混合整数规划模型、集合划分模型等。
(3)动态规划方法是解决多阶段决策过程中最优化组合的一种系统化方法。动态规划是美国数学家R.Bellman等人于20世纪50年代初开发出来的一个新的数学分支。
2.2 新组建船队的规划问题
求解这一类问题可以用线性规划法与动态规划法。线性规划法的思想是建立考虑时间因素的航线配船线性规划模型,用线性规划算法求解的方法,这种算法简单明了,但求得的最优方案中每年的造(购)船数不为整数的问题,与实际情况有差异;为弥补这一点,对其中一些变量加入整数约束,采用混合整数规划的求解算法,这样求解的每年的造(购)船数就一定为整数;但是,求解混合整数线性规划模型的算法收敛速度慢,计算时间取决于整型变量的多少。当整型变量的数目不多时,还有可能在较短的时间内求得最优解;反之,求得全局最优解是一件非常困难的事,只能通过对问题本身的深入理解,并巧妙地运用一些程序技巧,去寻求一个较为满意的局部最优解。因此,对于给定的船队规划问题,是否可能采用混合整数优化算法求解,需要慎重推敲才能确定。而采用单纯形算法求解最优方案通常总是最方便和最经济的。
2.3 船队规划模型
从本次船队规划问题的特点看,属于动态规划问题,可以转化为线性模型用线性算法和混合整数算法求解,也可以采用动态规划模型求解。本次船队论证规划方法采用了线性规划模型然后用混合整数算法求解。
2.3.1 设计变量
船队规划模型中以研究期内每一年各条航线上的各条船型的数量和各年新增的船型与数量为设计变量,通过求解设计变量来得到各年的最优配船方案。
2.3.2 目标函数
模型的建立以2012~2015年4年船队总营运成本现值为目标函数。
船舶营运成本分成两部分,固定成本和航次成本。固定成本包括年度折旧费和船员费用、年维修费、保险费等船舶营运过程中每年固定不变的成本;而航次成本包括燃润料费用、港口使费等营运费用中的随不同航线运量而变动的成本。
2.3.3 约束条件
(1)运量约束条件。转运量要满足各小型LNG接收站的转运量需求。
(2)船队发展连续性约束条件。当年各航线上运营与闲置的某船型艘数总和等于当年年初该型船舶艘数与新添置该船型艘数之和。
(3)变量非负性约束条件。与实际相符,模型中的决策变量,如某航线上某船型的艘数为非负值。
(4)整数约束条件。模型中新添置船数为整数。
3 组合优化方法
深海养殖与加工基地论证的核心问题有两个,一是如何配船,这可以使用组合优化方法中的装箱模型;二是如何规划船队每个船舶的航线,这是经典的TSP问题。
经典的一维装箱问题(BinPacking Problem)是指,给定件物品的序列,物品的大小,要求将这些物品装入单位容量1的箱子中,使得每个箱子中的物品大小之和不超过1,并使所使用的箱子数目最小。

图1 装箱模型算法的伪代码
TSP问题至今还没有有效的算法,是当今图论上的一大难题。目前只能给出近似算法,其中之一是所谓“改良圈算法”,即已知是G的Hamilton圈,用图2所示的算法把它的权减小。

图2 TSP算法伪代码
4 算例验证
2016~2019年,某深海养殖与加工基地的各一级站与二级站相继建成投产,拟组建由500吨渔船和1200吨渔船所组成的小型船队来完成2016~2019年的渔获转运任务。现要求:经过详实的市场调研及缜密的经济分析,提出经济性好、可操作性强,既不造成资源的浪费,又能满足市场需求的基地论证方案。
4.1 设计变量
xjht为设计变量,表示t年在h航线上航行的j型船的数量;Cjb为设计变量,表示b年新添置j型船舶的数量。
4.2目标函数

(4)整数约束条件。
Cjt为整数,t年添置j型船舶的数量为整数。
综合采用装箱模型和TSP模型,得到深海养殖与加工基地规划见表1。
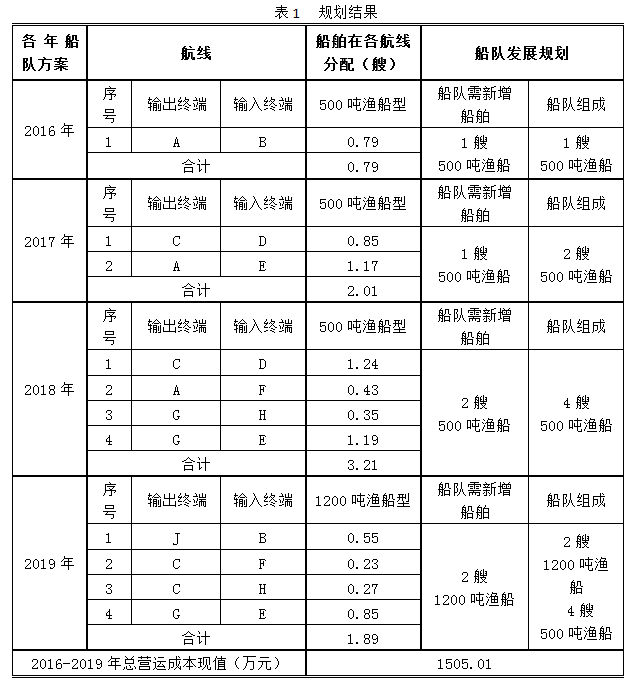
5 结论
基于已阐明的各项假定,以四年总营运成本现值最小作为目标函数,建立规划模型,根据分析实际情况建立约束条件,使用组合优化方法求解了2016~2019年深海养殖与加工基地逐年最优构成这一动态规划问题,提出了一套规划方案,该方案是经济性良好并且可行的方案。
参考文献
[1]孔飞.我国海洋牧场开发的相关问题探讨[J].大科技,2015,12(4).
[2]麦康森.深海养殖与海洋经济可持续发展[J].新经济,2014,(4).
[3]Richard B. Chase,Nicholas J. Aqnilano,F.Robert Jacobs.Operations Management ForCompetitive Advantage[J].China Machine Press,2001,(9).
[4]Schmitz,J,Platts,K.W.Supplierlogistics performance measurement:indication from astudy in the automotive industry[J].InternationalJournal of Production Economics,2004,89(9).
[5]E11ram,L.M.Supply management's involvement in the target costing process[J].European Journal of Purchasing& Supply Management,2002,8(4).
[6]邵飞牛.一维装箱问题启发式算法的设计与分析[D].沈阳:东北大学,2013.
[7]胡中华,赵敏.基于人工蜂群算法的TSP仿真[J].北京理工大学学报,2009,29(11).
[8]王宇平,李英华.求解TSP的量子遗传算法[J].计算机学报,2007,30(5).
(盖州市第一高级中学)








