1 引言
房价受到众多因素的影响,对于如何分析房价与各要素之间的关系,学者采用或提出了众多的方法与模型,如线性回归模型、灰色马尔科夫模型、空间计量模型、时间序列分析法、地理加权回归模型等。这些模型各有相应的优缺点,针对不同的现实情况其结果存在适用性。但就房价而言,其受到时间、空间、政策、社会心态等各种因素的影响,是一种极其复杂的因变量。其中,房屋地理位置作为一种地理信息,在房价上具有明显的影响,但如果仅仅采用一般的回归(如最小二乘法),每种影响要素的系数大小是固定的,即假定了房价受各因素的影响强度和空间位置无关,这实际上忽略了房屋作为一种地理要素的空间异质性——也就是说,各种影响要素的系数大小在不同的空间位置上实际上是不一样的。地理加权回归(Geographic Weighted Regression,GWR)是一种考虑了空间异质性的回归模型,在过去的十几年中,被广泛使用在各种空间要素的测算上。本文以重庆为例,采用地理加权回归模型,研究了重庆房价与各影响要素之间的关系。同时研究表明,采用GWR模型比一般的回归模型在房价分析预测上具有较好的优势。
2 数据与方法
2.1 研究对象
重庆位于中国内陆西南部、长江上游地区。幅员面积8.24万平方千米,辖38个区县(26区、8县、4自治县)。户人、城镇化率62.6%。重庆是中国四个直辖市之一,是西南地区和长江上游最大的经济中心城市。2017年,全市实现地区生产总值19500.27亿元。不同于北京、上海与天津三个直辖市,重庆的房价相比来说较低。
2.2 数据来源
在本文中,采用了多种数据,包括历年的平均房价数据、分区县房价数据、小区历年房价数据、人口、经济、教育条件、中心商业区等。这些数据的来源,包括《重庆市统计年鉴》、《中国城市统计年鉴》等统计数据,安居客、链家、房天下等多种网络公开数据,其他辅助数据包括重庆市卫星影像地图等。
2.3 GWR模型

在本文中,运用ArcGIS软件里的地理加权建模模块进行建模,选取高斯函数作为权重函数和采用信息准则(AIC)法确定的模型带宽。
2.4 数据预处理
对于这些数据,进行了相应的数据预处理工作,包括对于异常点数据、空缺数据等进行相应的处理。在数据的处理过程中,采用了Excel、MATLAB等进行数据的整理与可视化,采用地理信息软件ArcGIS等进行了数据在地理上的可视化。
2.5 影响要素选择
本文选用以小区为单位进行研究分析。样本数总量为1501个相关小区二手房信息,时间点为2018年2月,其主要集中在重庆主城区。对于小区的相关二十多个字段,首先进行自相关检验,通过方差膨胀因子(VIF)判定多重共线性。
之后,通过逐步选择法选择自变量(覃文忠,2007)。在经过一系列计算后,文章选用以下要素作为房价的影响因素:
(1)DisSubway:与最近地铁站的距离。
(2)WLoad:小区前面道路的宽度。
(3)IfSchoolHouse:是否为学区房,取值为0或1。
(4)BusinessLevel:最近商圈的等级,等级采用1-5量化。
(5)DisBusinessLevel:距离最近商圈的距离。
(6)AGDP:人均GDP,以区县为单位统计。
(7)DOP:人口密度,以区县为单位统计。
(8)GreenRate:小区绿化率。
(9)NetPopIn:人口净流入,以区县为单位统计。
(10)HaveBuildYears:房龄。
房价作为因变量,以小区为单位统计。
3 基于GWR模型的房价分析
如前所述,在房价分析上目前通常采用传统的最小二乘法(OLS)方法忽略了空间异质性的影响。而GWR模型充分考虑了各影响强度与空间位置的关系,较为全面考虑了空间异质性关系,与传统方法相比有明显优势。
3.1 GWR模型构建
为了分析重庆市房价与各影响因素的空间非平稳性关系,将2.5节的变量代入式2,构建GWR模型。由于本文研究的小区在地理上的聚集分布,所以此处采用调整型的空间核,空间权重函数采用双重平方权重函数,以AICc作为衡量标准,采用黄金分割搜索的方法来搜寻使得AICc最小的带宽方法,从而确定最佳近邻点。
通过计算,得到模型各参数在不同位置上的分布。为便于展示,本文将其利用ArcMap进行了可视化,并将点数据通过克里金插值为连续分布的面数据,更加符合现实情况。本文采用了10个自变量,故会有10幅表示影响要素的系数的空间分布图,限于篇幅,本文仅展示其中两幅(图1)。
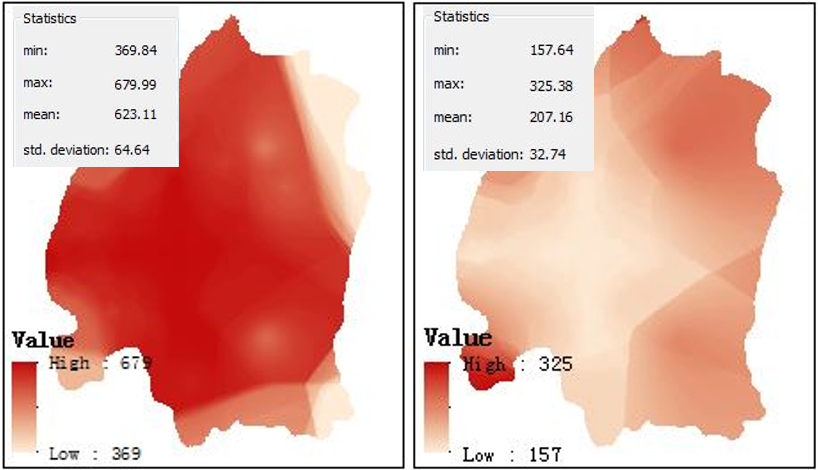
图1 IfSchoolHouse系数分布(左)与BusinessLevel系数分布(右)
为便于GWR模型较传统OLS回归模型的优势,本文同时将2.5章节的变量带入式1,得到了OLS回归模型的相关参数。二者对比见表1。
表1 GWR模型与OLS模型检验参数对比
|
| GWR | OLS | GWR Improvement |
| Sigma | >1×106 | 5230 |
|
| AICc | 42003 | 54231 | 12228 |
| R2 | 0.876 | 0.740 |
|
| Adj R2 | 0.825 | 0.713 | 0.112 |
| F(R2) | 14.6 | 77.3 |
|
| P-Value(R2) | 0 | <0.01 |
|
从GWR的与OLS模型的各项统计指标的比较可知,GWR模型相较于OLS模型有了较大程度的改进。OLS的调整后R2为0.713,而GWR中则改进到了0.825;F检验的显著性也表明GWR比OLS要出色;在最为重要的指标AICc上,GWR模型比OLS要低,这说明GWR反映的实际情况要比OLS好。
3.2 GWR结果分析
相较于OLS模型对于重庆市房价的影响因素给出全局的影响因子不同,GWR模型给出的是变化的影响因子。对于房价的前述影响因素,量化分析如下:
3.2.1 距离最近地铁站的距离(DisSubway)
对于地铁对房价的影响,在重庆主城九区,其影响因子平均为-6(即距离每增加10米,房价相应减少6元)。在中心城区,其可以达到-14左右,这说明地铁对于中心城区的影响要比周围城区要高,考虑到重庆市地铁在中心城区分布更密集,所以中心城区的人更在乎是否拥有地铁;而对于城市外围,很多地方并没有地铁站,所以对地铁的响应会比较小。
3.2.2 小区前道路的宽度(WLoad)
小区前主干道的宽度体现了小区的交通通行能力,对于重庆主城九区,其影响因子平均为53.6(即马路每加宽1米,房价增长53.6元)。在九个区内,其影响因子变化范围不大,为50~61,这说明道路的影响在整个区域是比较稳定的,但仍然可以看出,中心城区对马路宽度的响应较小,而周围城区对马路宽度的响应较大,这可能说明,在城区道路本来就更加拥堵,同时由于拥有轨道交通等通行方式,所以对马路的依赖略小。
3.2.3 是否为学区房(IfSchoolHouse)
学区房影响着住户的孩子的上学问题,从图中可以看出,其平均影响为623,即学区房会使得房屋价格增长623元,在主城九区,其变化从370~680,在中心城区,房价更能被学区房影响。
3.2.4 商圈等级(BusinessLevel)
商圈对于人们的生活具有很大的便利作用。本文将商圈等级划分为1~5,可以看出,商圈等级越高,对房价影响越大,其提高一个等级,可使得房价平均增长207元。同时,在中心城区对商圈的相应要比周围城区小,这可能由于中心城区本来商圈就多(密度大),而周围城区,在生活便捷度不如中心城区的情况下,更会依赖相应商圈。
3.2.5 距离最近商圈的距离(DisBusinessLevel)
显然,距离商圈越近,房价应该越高,在整个区域,距离商圈每增加10米,房价平均减少12元左右,同时,在整个区域其参数变化不大,但中心城区的依赖度更大一些。
3.2.6 区县人均GDP(AGDP)
一般来说,人均GDP高的地方,其生活成本(人力服务成本)也会较高,房价也会较高,这在主城九区也可体现。人均GDP对房价的影响约为285~478元/万元GDP,同时,GDP越高的地方,其响应参数也要大一些。
3.2.7 人口密度
人口密度体现了人口的聚集程度,也往往能代表着小区的楼层高度、楼宇密度、入住率、容积率等多种信息,其现实解释较难。但在本模型中,我们可以看出其与房价呈正相关性,且中心城区对人口密度的响应更大。
3.2.8 小区绿化率(GreenRate)
小区绿化率高,说明小区的环境更好。绿化率每提高一个百分点,房价约增加6元。在整个区域,其变化为3.4~14,中心城区的房子对于绿化率的响应更大。
3.2.9 人口净流入(NetPopIn)
当一个地方人口净流入时,往往以为着房屋的需求更大。在重庆九区,人口每净流入1万人,房价约增长28元。且中心城区对人口净流入的响应更高,这或许因为中心城区房屋供应更少,所以更能响应。
3.2.10 房龄(HaveBuildYear)
房龄越大,说明房屋越旧。一般来说,新房的房价会更高,在整个区域,房龄每增加1年,房价约降低120余元,且整个区域对房龄的响应基本一致。
4 结论与展望
本文采用GWR模型分析了重庆房价与多种影响因素之间的关系,详细阐述了10个影响要素在重庆不同地区的系数大小与差异分析。相比于传统OLS方法,GWR在对于房价这种具有空间异质性的要素分析上具有较大的优势。在以后的研究中,研究人员应充分考虑地理空间要素所表现的空间异质性,从而才能更好地分析不同要素对于房价的影响或者房价的未来走势。
参考文献
[1]王新刚.城市住房价格时空模型分析[D].开封:河南大学,2015.
[2]覃文忠.地理加权回归基本理论与应用研究[D].上海:同济大学,2007.
[3]覃文忠,王建梅,刘妙龙.混合地理加权回归模型算法研究[J].武汉大学学报(信息科学版),2007,(2).
[4]徐聪.北京市房价的GWR模型与空间结构分析[D].北京:中国人民大学,2011.
(重庆市第八中学校)








